Resultats de la cerca
Es mostren 31 resultats
catenària
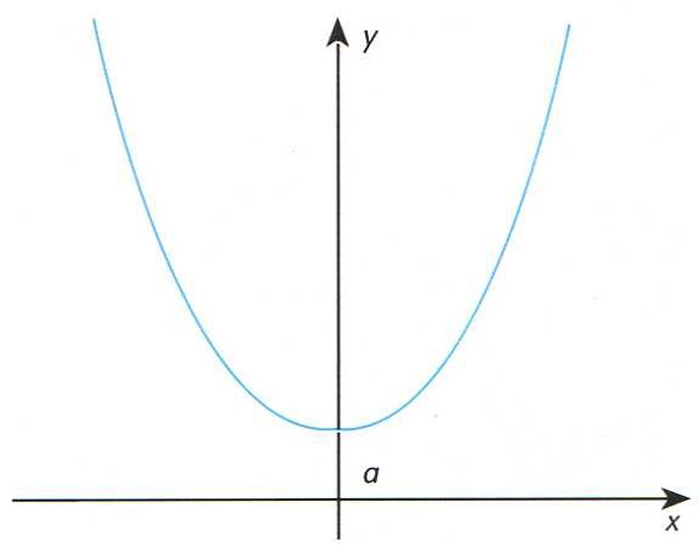
La major o menor concavitat de la corba depèn de la separació dels punts extrems (que es determinen pel paràmetre a de la seva equació)
© fototeca.cat
Matemàtiques
Corba que adopta una cadena, corda, etc, perfectament flexible i amb una càrrega uniformement repartida en tota la seva llargària, fixa en els seus extrems i suspesa lliurement.
L’expressió matemàtica d’aquesta corba és donada per l’equació y=achx/a , on a és la distància des del punt més baix de la corba a l’eix d’abcisses de referència
bisectriu
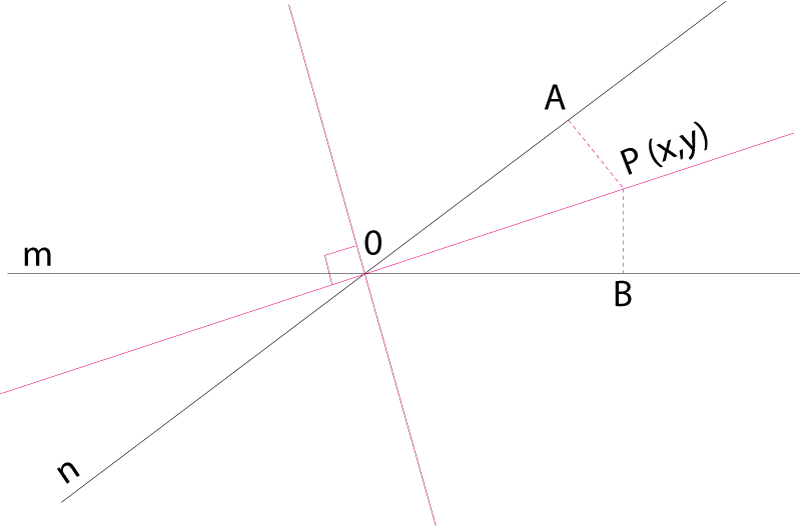
Bisectrius corresponents als quatre angles determinats per dues rectes que es tallen
© Fototeca.cat
Matemàtiques
Lloc geomètric dels punts que equidisten dels costats d’un angle, el qual divideix, per tant, en dos angles iguals.
Dues rectes que es tallen determinen quatre angles, iguals dos a dos Llurs bisectrius són dues rectes perpendiculars entre elles En considerar un dels quatre angles hom distingeix la bisectriu interior i la bisectriu exterior Les equacions de les bisectrius dels angles que determinen dues rectes que es tallen, les d’equacions de les quals són, en una referència cartesiana normal, A 1 x + B 1 y + C 1 = 0 i A 2 x + B 2 y + C 2 =0, són
bisector
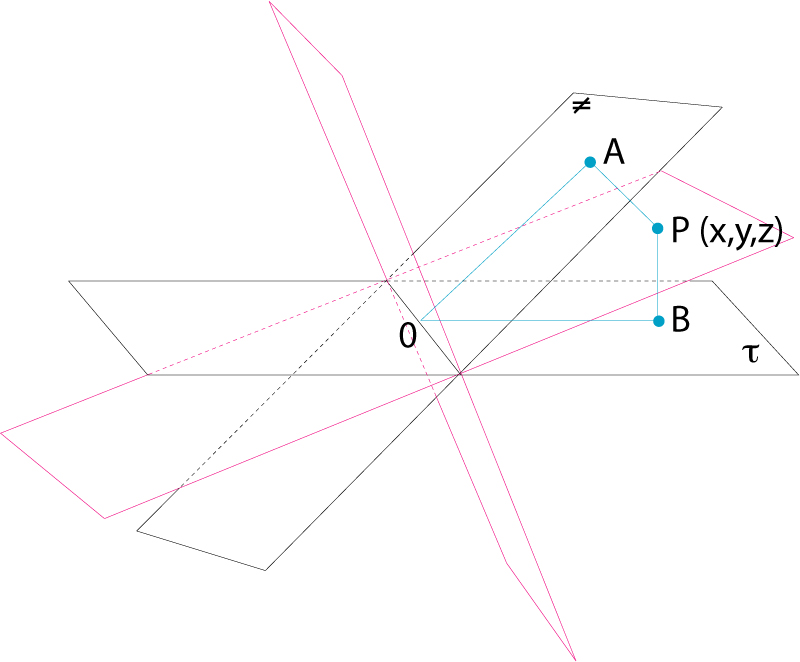
Plans bisectors dels quatre díedres formats per dos plans donats que es tallen
© Fototeca.cat
Matemàtiques
Lloc geomètric dels punts que equidisten dels dos plans costats d’un angle díedre, el qual, per tant, és dividit en dos díedres iguals.
Dos plans no parallels determinen quatre angles díedres, per als quals hom distingeix dos plans bisectors Per a cada díedre, un dels plans bisectors serà interior, i l’altre, exterior Si les equacions cartesianes de dos plans són A 1 x + B 1 y + C 1 z + D 1 = 0 i A 2 x + B 2 y + C 2 z + D 2 = 0, en una referència cartesiana normal, l’equació dels dos plans bisectors dels díedres que aquells determinen és
ortodromia
Matemàtiques
Cartografia
La línia de menor longitud de totes les que passen per dos punts donats de la superfície terrestre.
Si hom admet que la Terra és perfectament esfèrica, l’ortodromia que uneix dos punts és l’arc de cercle màxim que els dits punts determinen loxodromia
altura
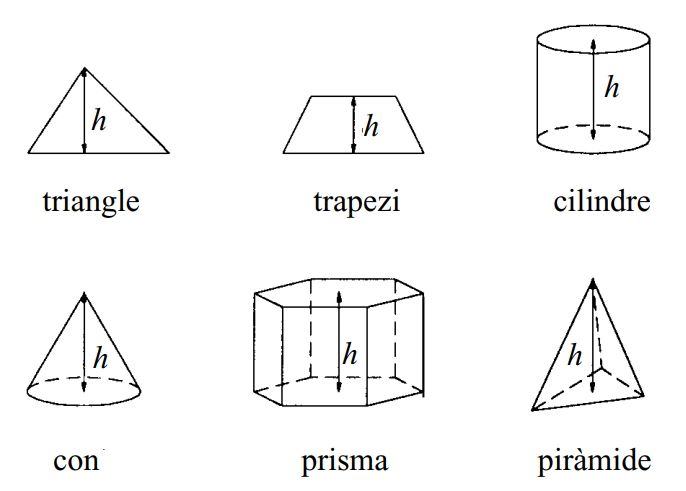
Altures de diferents figures i cossos geomètrics
© Fototeca.cat
Matemàtiques
Segment de recta (o també la seva longitud) en les figures i en els cossos geomètrics comprès entre dos de llurs elements (un vèrtex i un costat al triangle, dos costats al paral·lelogram) i perpendicular almenys a un d’aquests elements, anomenat base, o bé a una recta o a un pla que els determini.
Moltes figures i molts cossos presenten diverses altures segons quin costat hom prengui com a base En un triangle, les tres altures es tallen en un punt dit ortocentre i els seus peus determinen el triangle òrtic
zona

Zona esfèrica
© Fototeca.cat
Matemàtiques
Porció de superfície esfèrica compresa entre les dues interseccions de dos plans paral·lels amb l’esfera.
L’altura d’una zona esfèrica és la distància perpendicular entre els dos plans que la determinen, i la seva àrea val 2π Rh , on R és el radi de l’esfera i h l’altura de la zona
tríedre
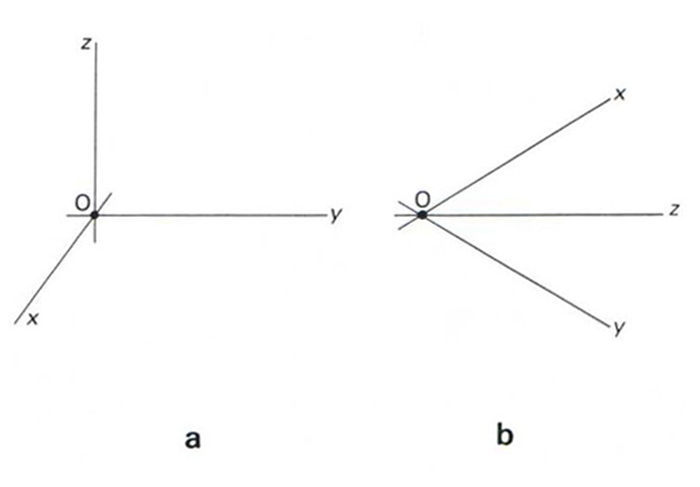
tríedre: a, triectangular; b, guerxo
© fototeca.cat
Matemàtiques
Figura formada per tres línies no coplanàries que es tallen en un punt.
Tot tríedre pot ésser descrit en termes de tres plans que es tallen en un punt i és la base per a utilitzar sistemes de referències amb coordenades És anomenat tríedre trirectangular si les línies que el determinen són perpendiculars
evolvent
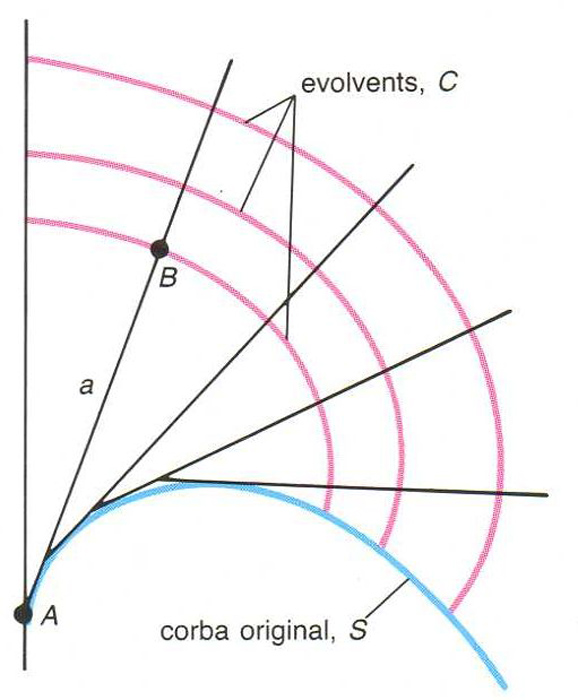
Les corbes C són les evovlents de S
© fototeca.cat
Matemàtiques
Donada una corba S
, cadascuna de les corbes ortogonals a les tangents de S
.
Si C és una envolvent de S , S és l'evoluta C Donada la corba S , hom pot generar una evolvent tot fixant una tangent a S en un punt de tangència A , limitant-ne la seva longitud a i anant-la enrotllant a la corba, de manera que el punt extrem B determina una evolvent Les diferents longituds a determinen les diferents evolvents
estructura algèbrica
Matemàtiques
Conjunt en què hom ha definit una o unes quantes relacions binàries o lleis de composició.
Una llei de composició interna definida en un conjunt E és una operació que permet de fer correspondre a cadascun dels parells ordenats a, b d’elements, distints o no de E , un element ben determinat del mateix conjunt E Així, doncs, una llei de composició apareix com una aplicació de E × E en E Una estructura és definida, doncs, per mitjà d’un cert nombre d’axiomes que determinen les relacions i les operacions que la componen Les estructures més freqüents en àlgebra són les de grup, anell, cos i espai vectorial