Resultats de la cerca
Es mostren 12 resultats
diagrama
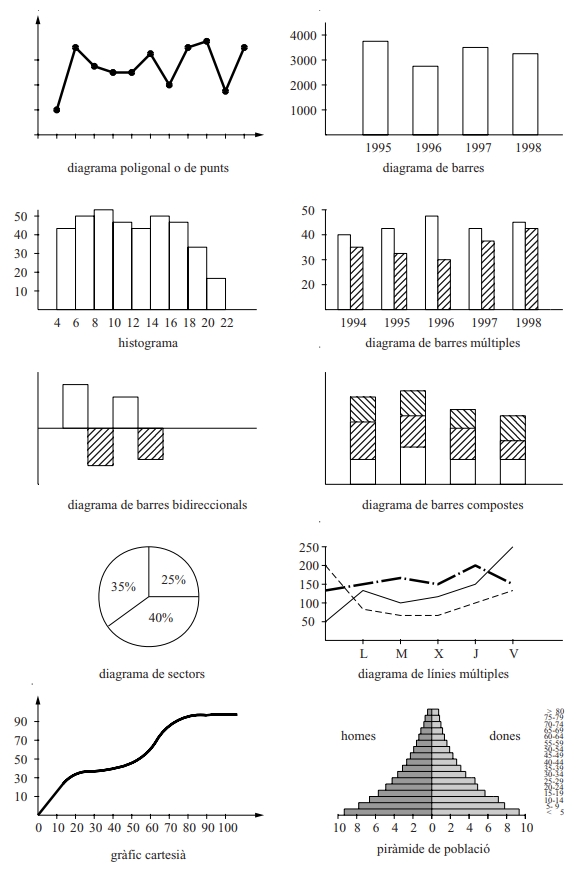
Diagrames estadístics: de barres, de sectors, etc,
Matemàtiques
Gràfic traçat generalment en un pla dotat d’uns eixos de coordenades per tal d’il·lustrar la relació existent entre dues quantitats variables, una de les quals hom pot considerar com a funció de l’altra.
diagrama de Venn
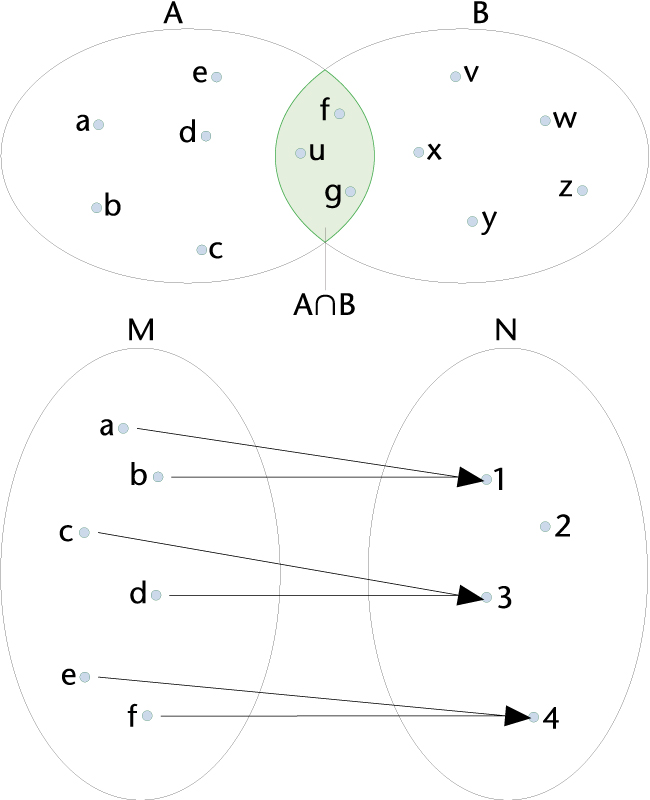
Representació de la intersecció dels conjunts A i B (a dalt) i de l’aplicació del conjunt M en el conjunt N (a baix) per mitjà de diagrames de Venn
© Fototeca.cat
Matemàtiques
Diagrama emprat amb fins didàctics per a representar gràficament conjunts i estudiar les relacions i operacions entre conjunts.
Aquests diagrames foren introduïts pel matemàtic i lògic anglès John Venn 1834-1923 Els conjunts són representats mitjançant cercles o corbes tancades qualssevol Cal no confondre un diagrama de Venn amb la regió del pla limitada pel diagrama És conegut també com a diagrama d’Euler-Venn
diagrama en arbre
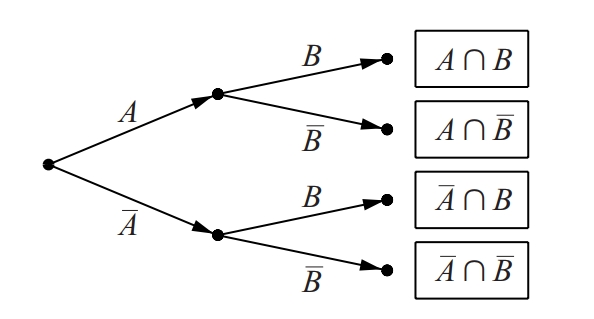
diagrama en arbre
Matemàtiques
Representació d’un sistema jeràrquic en un arbre, de manera que el grau de jerarquia s’expressa col·locant els elements en branques més o menys properes a l’arrel.
diagrama d’Argand
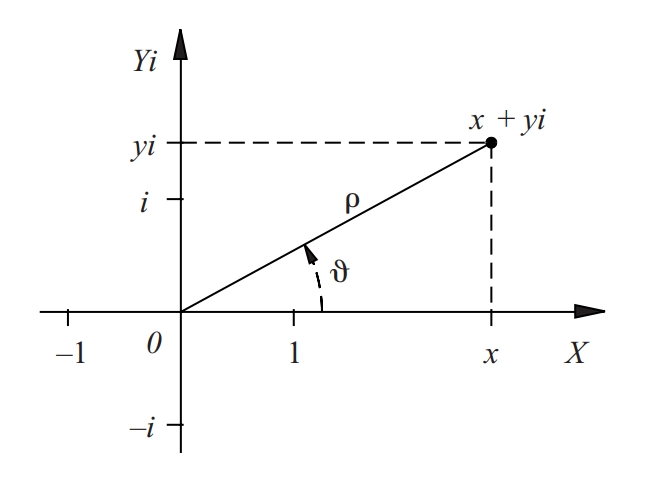
diagrama d’Argand
© fototeca.cat
Matemàtiques
Representació d’un nombre complex x + yi pel seu afix del pla (x,y), la qual cosa permet vissualitzar els nombrres complexos.
diagrama d’Euler-Venn
Matemàtiques
Representació gràfica d’un conjunt o d’una operació entre conjunts.
núvol de punts
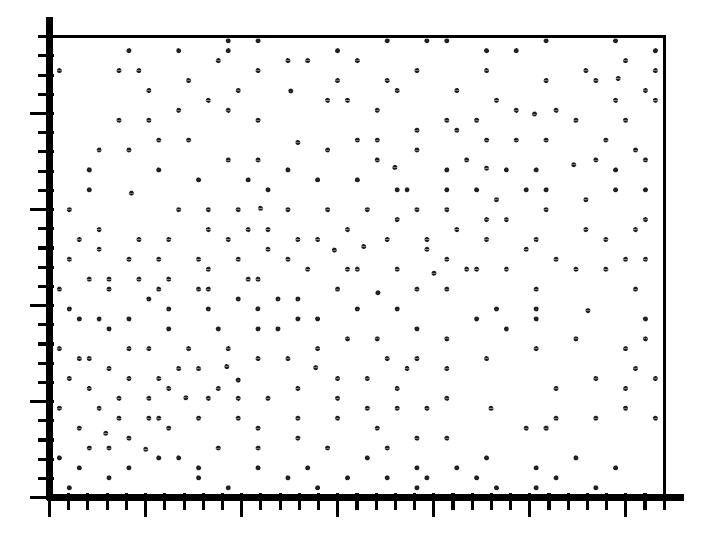
núvol de punts
Matemàtiques
Conjunt de punts del pla o de l’espai que visualitzen els valors de diverses variables estadístiques la dependència de les quals es vol estudiar.
correlació
Matemàtiques
Grau d’interdependència entre diverses variables o, dit d’una altra manera, entre diferents conjunts de nombres.
Si els valors de les diferents variables satisfan exactament una equació, hom diu que hi ha una correlació perfecta entre elles Quan hi ha dues variables, és anomenada correlació simple , i si el nombre de variables és superior a dues, correlació múltiple Donades dues variables aleatòries X , Y , la localització dels parells de punts X, Y damunt un sistema de coordenades rectangular rep el nom de diagrama de dispersió Si tots els punts del diagrama semblen trobar-se aproximadament damunt una recta, hom diu que la correlació és lineal quan els punts descriuen amb…
autòmat finit
Matemàtiques
Electrònica i informàtica
Model matemàtic d’un sistema que té un nombre finit d’estats d’entrada i de sortida —els quals representen les diferents configuracions de signes (i estats interns) que representen la capacitat que té el sistema d’enregistrar els esdeveniments passats— i en el qual l’estat de sortida depèn en qualsevol moment de l’entrada present i dels estats interns.
Per tant, un autòmat finit es defineix pel conjunt finit dels estats d’entrada, de sortida i interns possibles per una funció que dóna el següent estat intern corresponent a un estat d’entrada i a un estat intern donats i per una funció que determina l’estat de sortida següent Aquest concepte és essencialment abstracte i té valor tant per a descriure programes com per a descriure aparells Un autòmat finit concret es defineix normalment per mitjà de la seva taula d’estats , que consisteix en una llista de les relacions existents entre els estats d’entrada, els de sortida i els interns Una…
autòmat finit determinista
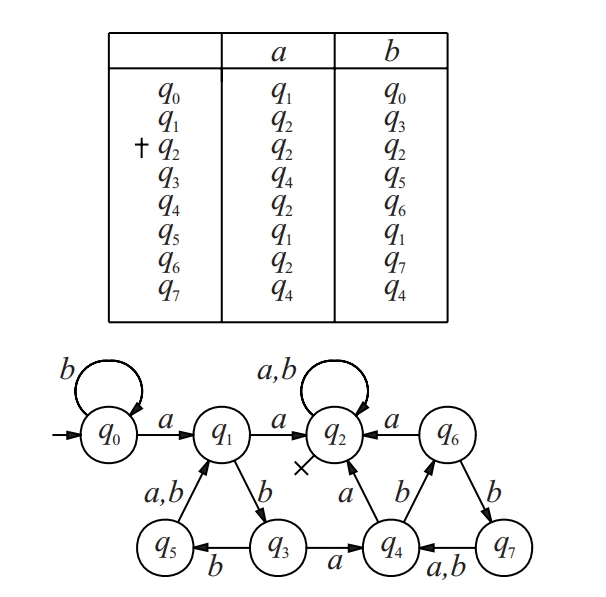
autòmat finit determinista
Matemàtiques
Estructura de la forma M = (Q, ∑, δ, q0, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet, anomenat d’entrada; δ : Q ⨉ ∑* → Q és la funció de transició que satisfà ∀q ∈ Q, ∀x,y ∈ ∑*:δ(q, λ) = q, δ(q, xy) = δ(δ(q, x), y) essent xy la concatenació de x i de y, i λ la paraula buida i ∑* el conjunt de paraules; q0 ∈Q s’anomena estat inicial; F ⊂ Q s’anomena conjunt d’estats finals o acceptadors.
Usualment un autòmat finit determinista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si δ q i , a = q j S’indica l’estat inicial amb una fletxa i els finals amb una creu
autòmat finit indeterminista
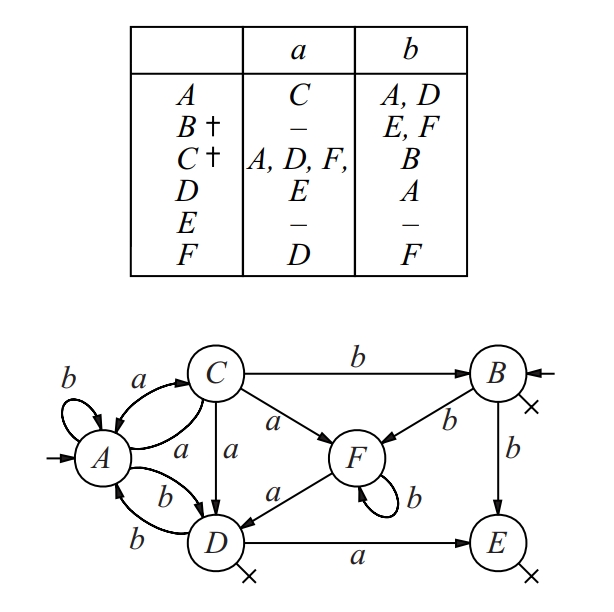
autòmat finit indeterminista
Matemàtiques
Estructura de la forma M = (Q, ∑, δ, I, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet anomenat d’entrada; δ : 2Q ⨉ ∑* → 2Q és la funció de transició que satisfà ∀P1, P2 ⊂ Q, ∀x, y∈∑*: δ(∅, x) = ∅, δ(P1, λ) = P1, δ(P1 ∪ P2, x) = δ(P1, x) ∪ δ(P2, x), δ(P1, xy) = δ(δ(P1, x)y), essent xy la concatenació de x i de y i ∑* el conjunt de paraules; I ⊂ Q és el conjunt d’estats inicial; F ⊂ Q és el conjunt d’estats finals o acceptadors.
Usualment un autòmat finit indeterminista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si q j ∈ δ q i , a S’indiquen els esstats inicials amb fletxes i els finals amb una creu Els llenguatges acceptats pels autòmats finits indeterministes són els mateixos que els reconeguts pels finits deterministes regulars L’avantatge dels indeterministes enfront dels deterministes és la facilitat de maneig i de construcció