Resultats de la cerca
Es mostren 9 resultats
espai normal
Matemàtiques
Espai topològic en el qual, donats dos espais tancats disjunts, n’hi ha dos d’oberts també disjunts que els contenen.
Un teorema d’Urysohn afirma que en un espai normal, donats dos espais tancats disjunts, hi ha una funció real contínua que pren el valor zero en l’un i el valor u en l’altre
axiomes de separació
Matemàtiques
Axiomes topològics relatius a les possibles separacions entre punts.
En un espai topològic Y , els axiomes són Axioma T 0 Per a qualsevol parell de punts x i y diferents, existeix un entorn de x que no conté y Axioma T 1 Per a qualsevol parell de punts x i y diferents, existeixen un entorn U de x , i un entorn V de y , tals que U no conté y i V no conté el punt x Quan aquest axioma se satisfà, l’espai es diu espai de Fréchet Axioma T 2 Per a qualsevol parell de punts x i y diferents, existeix un entorn de x i un entorn de y sense punts en comú Quan aquest axioma se satisfà, l’espai s’anomena espai de Hausdorff Axioma T 3 Per a cada punt x i tot conjunt…
mesura
Matemàtiques
Aplicació m definida entre una àlgebra de conjunts ɑ d’un espai mesurable (Ω, ɑ) i el conjunt ℝ+ dels nombres reals positius.
L’aplicació compleix que la mesura de la unió de dos conjunts A i B de ɑ és igual a la suma de les respectives mesures, és a dir ∀ A ∈ ɑ i ∀ B ∈ ɑ tals que A ∩ B = ∅, m A + m B La terna Ω, ɑ, m és anomenada espai de mesura , i els conjunts de l’àlgebra ɑ són anomenats mesurables En el cas que ɑ sigui una σ-àlgebra de Borel, una mesura m és anomenada σ-additiva si la mesura d’una unió infinita i numerable de conjunts de ɑ disjunts dos a dos és igual a la suma de les respectives mesures, és a dir essent A i ∈ ɑ i A i ∩ A j = ∅, per a tot i, j tals que i ≠ j Una mesura és anomenada fitada…
volum
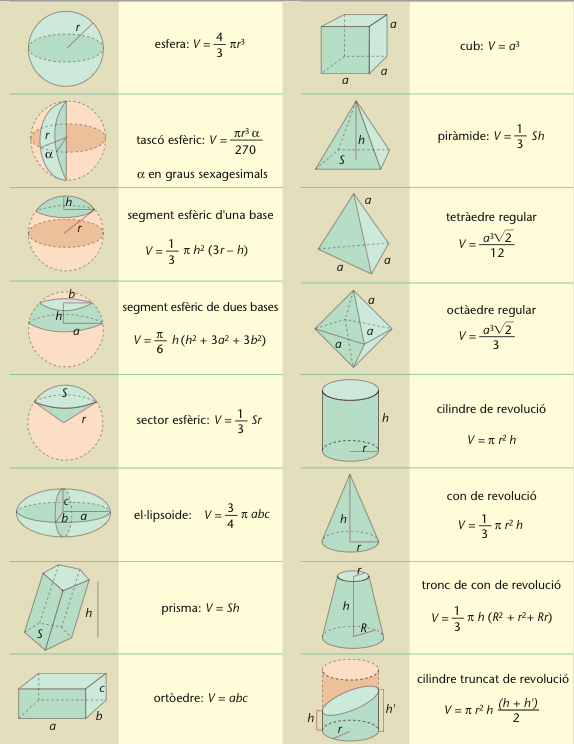
Fórmules per al càlcul de volums
© Fototeca.cat
Matemàtiques
Grandor o mesura de la porció de l’espai ocupada per un cos.
El volum és una mesura que a tota regió de l’espai de tres dimensions assigna un nombre real positiu, de manera que es compleix la propietat additiva, és a dir, que el volum d’un cos és igual a la suma dels volums de qualsevol partició que hom hagi fet en el cos divisió del cos en parts disjuntes Prenent com a base que el volum assignat a un cub de costat a és a 3 , el volum de qualsevol altre cos pot ésser calculat com l’ínfim de la suma dels volums dels cubs disjunts que plegats cobreixen el cos Així, el volum d’una figura plana és zero El volum dels cossos geomètrics simples…
nansa
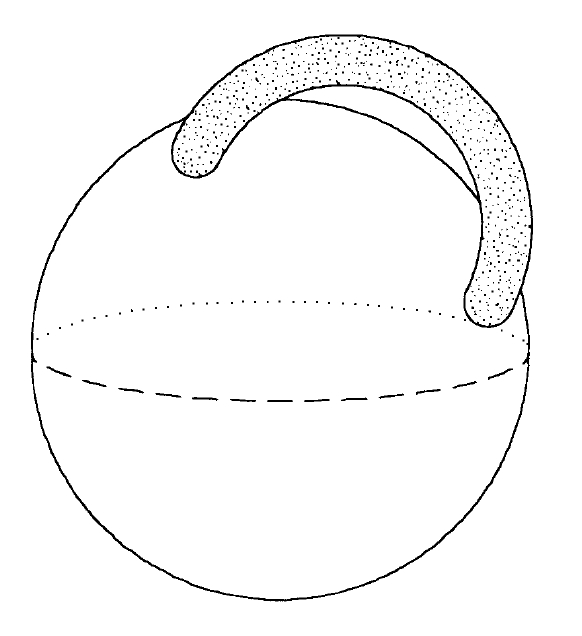
nansa
Matemàtiques
Peça d’una superfície construïda identificant dos discos disjunts sobre una altra superfície com a extrems d’un cilindre.
bipartit | bipartida
Matemàtiques
Dit d’un graf que té el conjunt de vèrtexs format per dos subconjunts disjunts, anomenats conjunts estables, i amb arestes que uneixen únicament vèrtexs d’un subconjunt amb vèrtexs de l’altre.
espai de Hausdorff
Matemàtiques
Espai topològic X que acompleix l’axioma de Hausdorff (o axioma de separació), segons el qual, per a qualsevol parell de punts distints x, y de X existeix un entorn de x i un altre de y que són disjunts.
És anomenat també espai separat Els espais euclidians de qualsevol dimensió són de Hausdorff
probabilitat
Matemàtiques
Concepte que permet d’expressar quantitativament el caràcter aleatori d’un esdeveniment o fenomen que hom creu que pot succeir.
El càlcul de probabilitats , branca de la matemàtica que presenta un gran nombre d’aplicacions científiques i tècniques, sorgí a França al s XVII amb els matemàtics B Pascal i P Fermat La motivació principal era l’estudi del guany esperat en els jocs d’atzar ruletes, daus, cartes, etc i, per tant, l’objectiu era el càlcul directe de la probabilitat utilitzant tècniques de combinatòria La noció de probabilitat en què hom es basava fou formulada l’any 1795 pel matemàtic francès P S Laplace de la següent manera “Si un fenomen pot produir un nombre de resultats diferents i igualment probables,…
conjunt

Representació gràfica de la relació de pertinença i de les operacions d’unió i intersecció dels conjunts
© Fototeca.cat
Matemàtiques
Reunió d’objectes ben definits en la intuïció o en el pensament, considerada com una totalitat (Cantor).
Aquesta definició, des del punt de vista matemàtic, no és vàlida, i, així, en matemàtiques la noció de conjunt no és definida, i s’inclou dins del desenvolupament d’una teoria axiomàtica que eviti les paradoxes i contradiccions com les que, a començament del segle XX, posaren en qüestió no solament la teoria de conjunts, sinó bona part de la matemàtica Hom no defineix, doncs, ni conjunt, ni element, ni la relació de pertinença, i es conforma amb la idea intuïtiva del que signifiquen frases com Un conjunt és format per elements, o l’element 4 pertany al conjunt dels nombres naturals La…