Resultats de la cerca
Es mostren 25 resultats
superfície
Matemàtiques
Conjunt de punts de l’espai que poden ésser determinats per dos paràmetres.
La manera més simple de determinar una superfície és donar una o més equacions del tipus z = f x,y Elegit un punt x,y en el domini de definició de la funció f , aquesta funció o aquestes funcions donen els valors de z , que, juntament amb x,y , són les coordenades cartesianes dels punts de la superfície Les funcions que donen la superfície esfèrica són , on el signe + correspon a l’hemisferi superior, i el signe - a l’hemisferi inferior L’equació z = ax + by + c correspon al pla o superfície plana Sovint és difícil, o impossible, d’expressar una superfície per…
axiomes independents
Matemàtiques
Conjunt d’axiomes tals que cap d’ells no es pot deduir dels altres.
Per a demostrar aquesta independència es donen models que satisfan certs axiomes, però no els altres
punt de contacte
Matemàtiques
Punt comú a dues corbes en el qual tenen la mateixa tangent.
Hom diu que aquest contacte M és d’ordre n si es donen dos punts P i P’ infinitament propers a M, un sobre cada corba, tals que la distància PP’ sigui un infinitèsim d’ordre n +1 respecte a l’arc MP i a la corda MP
analogies
Matemàtiques
Fórmules de resolució de triangles esfèrics, emprades generalment per a comprovar els resultats trobats per altres mètodes (grups de Bessel, etc.).
Hom distingeix les fórmules trobades per Neper 1614 que donen el valor de tg 1 / 2 A + B, tg 1 / 2 a + b, tgs41/ 2 A - B, tg 1 / 2 a - b i les de Delambre i Gauss 1808, que relacionen els angles d’un triangle esfèric amb els costats oposats
dual
Matemàtiques
Dit de dues nocions matemàtiques que, permutades en l’enunciat d’un teorema, donen lloc a un nou teorema.
Per exemple, la intersecció i la unió són duals, ateses les lleis de De Morgan
nombres poligonals
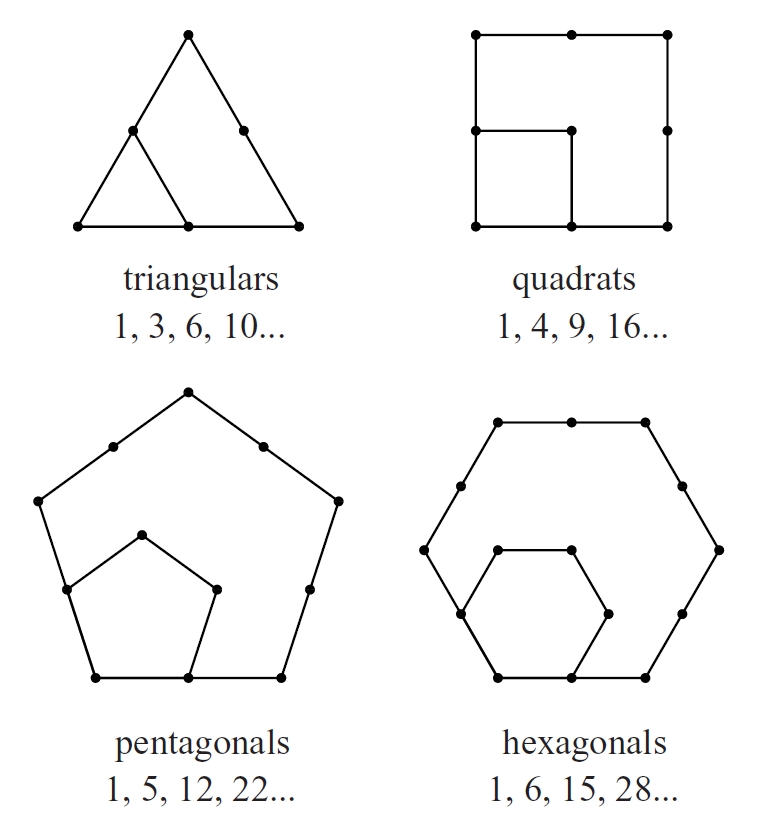
Nombres poligonals
Matemàtiques
Nombres que donen la quantitat de boles que hom pot disposar formant un triangle equilàter (nombres triangulars), un quadrat o bé qualsevol polígon regular.
problema
Matemàtiques
Tota qüestió en què partint d’unes dades conegudes cal arribar a uns resultats.
El resultat d’un problema pot ésser de natura molt diversa cal distingir, dins la matemàtica, els problemes de calcular, els problemes de construir i els problemes de demostrar En els problemes de calcular , és possible que per analogia amb altres problemes ja coneguts hom pugui aplicar unes regles que donen directament la solució, que pot constar d’un o més nombres Quan aquestes regles no són fàcils de descobrir hom recorre a expressar algèbricament les condicions de l’enunciat, és a dir, expressar per mitjà d’equacions les relacions entre les dades i les incògnites del problema si aquestes…
simetria
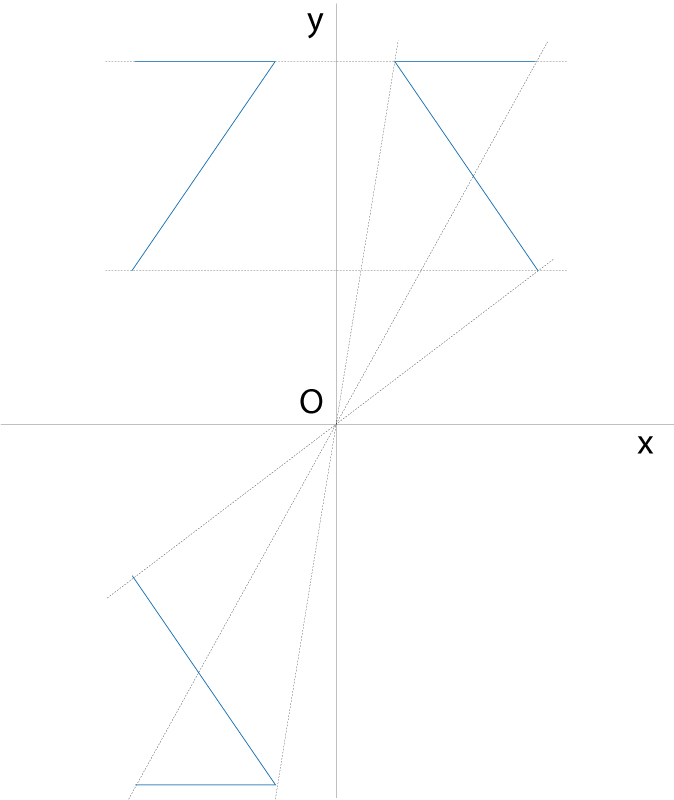
Dues figures obtingudes per simetria axial i central
© Fototeca.cat
Matemàtiques
Configuració d’un objecte que és invariant per a determinats moviments geomètrics.
Dins el concepte de simetria hom estudia modernament tots el moviments geomètrics del pla i de l’espai Una simetria axial és la transformació que per a tot punt P n'assigna un altre P' , de manera que la recta PP' és perpendicular a una recta donada dita eix de simetria i les distàncies de P a l’eix i de P' a l’eix són iguals Una simetria especular és la transformació que per a tot punt P n'assigna un altre P' , de manera que la recta PP' és perpendicular a un pla donat dit pla de simetria i les distàncies de P al pla i de P' al pla són iguals Una simetria central és una rotació de 180°…
teorema de Stokes
Matemàtiques
Teorema segons el qual, donada una regió R, amb frontera C i superfície S, en què es donen certes condicions de regularitat, se satisfà que , on F és un camp vectorial sobre R.
equació diferencial de Bessel
Matemàtiques
Nom donat a l’equació diferencial x2y’’ + xy’ + (x2-ν2)y = 0, essent ν un nombre complex qualsevol.
Resulta d’expressar l’equació de Laplace, ∇ 2 ψ x, y, z = 0, en coordenades cilíndriquesquan és possible d’aplicar a la funció ϕ el mètode de separació de variables ϕ x , y , z = X x Y y Z z Una sollució particular de l’equació de Bessel és la funció de Bessel de primera classe , d’ordre ν on Γ és la funció gamma J - ν x n'és també solució particular Si n és enter, la corresponent funció J n x pot ésser estesa a tot ℂ si ν no és enter, J ν x pot ésser estesa a ℂllevat de l’eix real negatiu Si n és enter, J - n x = -1 n J n x en canvi, si ν no és enter, J ν x i J - ν x…