Resultats de la cerca
Es mostren 5 resultats
envolupant
Matemàtiques
Corba tangent a totes les d’una família, cadascuna de les quals és anomenada involuta
.
Donada la família de corbes f x,y,h = 0, hom calcula l’equació de l’envolupament eliminant el paràmetre h entre l’equació de la família f x,y,h = 0 i la derivada respecte a h, f' h x,y,h = 0 El concepte d’envolupant també pot ésser aplicat a una família de superfícies
evoluta
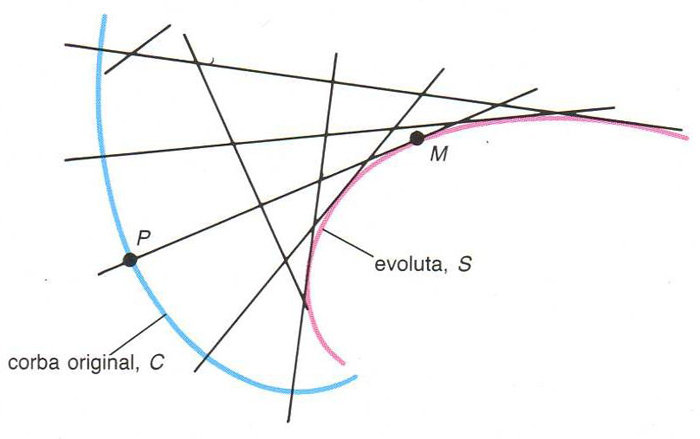
La corba S és l’evoluta de C
© fototeca.cat
Matemàtiques
Donada una corba plana C
, lloc geomètric dels centres de curvatura de C
.
És l'envolupant S de les normals a la corba C així, una normal en el punt P a C és tangent a l’evoluta i el punt de tangència M és el centre de curvatura de C en el punt P Si S és l’evoluta de C , C és una evolvent de S L’evoluta d’un cercle es redueix a un punt
subespai
Matemàtiques
Qualsevol subconjunt no buit F d’un espai vectorial E (sobre un cos K) tal, que és estable per a les dues lleis de E i que, proveït d’aquestes lleis induïdes, és també un espai vectorial (sobre K).
En l’espai vectorial de tres dimensions ℝ 3 els subespais són el mateix espai, l’origen de coordenades i totes les rectes i els plans que passen per l’origen F és un subespai de E si, donats qualssevol x , y de F i λ de K , aleshores la combinació lineal x ,-λ y pertany a F Tota família de vectors determina l’anomenada envolupant lineal , o mínim subespai, que els conté La intersecció M ∩ N de dos subespais M i N és un subespai, però la reunió M ∪ N no ho és en general La suma M + N definida per a tots els vectors que són suma d’un element de M i un de N és el mínim subespai que…
oloide
Matemàtiques
Envolupant convexa de dues circumferències ortogonals d’igual radi que passen l’una pel centre de l’altra.
involuta
Matemàtiques
Donada una corba C, cadascuna de les corbes de la família de la qual C és l’envolupant
.