Resultats de la cerca
Es mostren 20 resultats
conjunt continu
Matemàtiques
Tot conjunt que té la potència del continu o, equivalent, que és equipotent al conjunt OOO(ℕ), que és el conjunt de les parts del conjunt ℕ dels nombres naturals.
La hipòtesi del continu estableix que no hi ha cap conjunt el cardinal del qual sigui superior al cardinal d’ℕ i inferior al cardinal de OOO ℕ
teorema d’Apol·loni
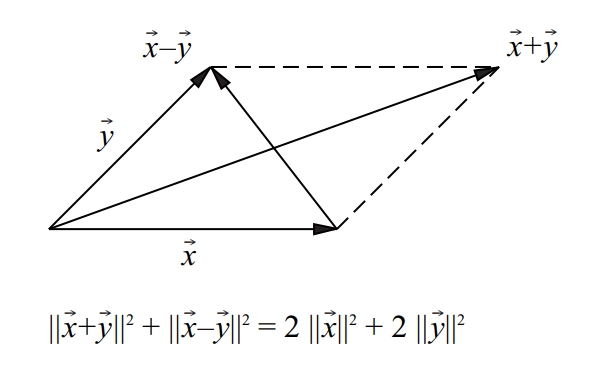
Formulació vectorial del teorema d’Apol·loni
Matemàtiques
Teorema de geomètria mètrica segons el qual en tot triangle la suma dels quadrats de dos costats és igual al doble de la suma del quadrat de la meitat del tercer costat més el quadrat de la mitjana corresponent a aquest darrer costat.
En la seva formulació actual, amb vectors i normes, aquest teorema s’anomena també llei del parallelogram i estableix que la suma dels quadrats de les dues diagonals del parallelogram és igual a la suma dels quadrats dels quatre costats
teorema de Bolzano-Cauchy
Matemàtiques
Teorema referit a l’estudi de la convergència de funcions.
Estableix que la condició necessària i suficient perquè la funció y x sigui convergent en x →η és que, per a cada nombre ε > 0, es compleixi per a tot parell de valors x’, x' d’un cert entorn reduït de η l’acotació | y x' - y x' | < ε Aquest teorema referit a la convergència de funcions és aplicat a la teoria de sèries quan la variable és natural i d’integrals
teorema de Tales
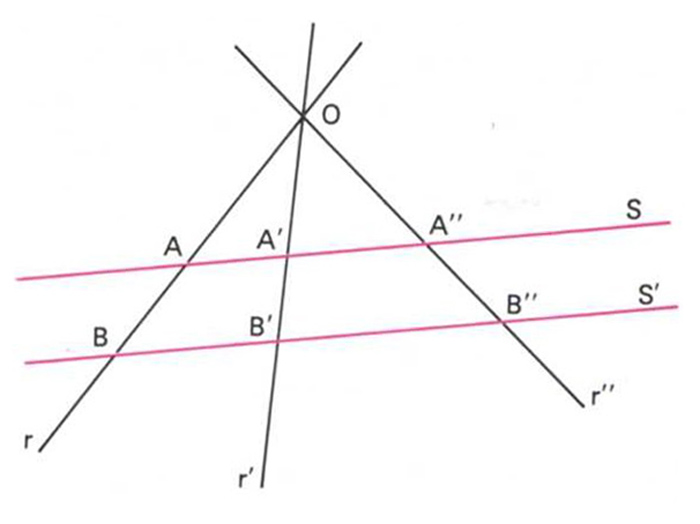
Teorema de Tales
© fototeca.cat
Matemàtiques
Teorema que estableix la proporcionalitat dels segments interceptats per rectes paral·leles sobre un feix de rectes concurrents.
Així, si tres rectes r, r´ i r’ que es tallen en O, són interceptades per les rectes paralleles en S, i en els punts B, B´ i B’ en S´, el teorema de Tales permet d’establir, entre d’altres, les següents relacions
director | directora
Matemàtiques
Que dirigeix el moviment d’un punt o d’una línia i n’estableix, així, la direcció.
llei dels grans nombres
Matemàtiques
Teorema intuït per Jakob Bernoulli i P.S.Laplace i batejat així per S.D.Poisson, la demostració del qual, progressivament més i més rigorosa, començà amb P.L.Čebyšev i ha acabat amb E.F.E.Borel, Khinčin, A.N.Kolmogorov, Glivenko i Cantelli.
Una primera formulació de la llei dels grans nombres és la llei feble dels grans nombres , anomenada també teorema de Bernoulli, que estableix que la freqüència relativa d’un esdeveniment al llarg de n temptatives elementals independents convergeix en probabilitat vers la probabilitat de l’esdeveniment Hom diu que una variable aleatòria X n convergeix en probabilitat vers una variable certa A quan la diferència | X n —A | tendeix a 0 en augmentar n , és a dir, quan ε essent tan petit com hom vulgui Una altra formulació de la llei dels grans nombres és l’anomenada llei forta dels…
problema de les paraules
Matemàtiques
Problema d'àlgebra.
D’una banda si hom disposa d’un alfabet finit OOO = {a 1 ,,a n } i, per concatenació, construeix els mots M = ζ 1 ζ r , on cada símbol ζ i és una de les lletres a j ∈ OOO d’aquest alfabet i r ∈ ℕ si, d’altra banda, hom disposa d’un cert diccionari que estableix l’equivalència de certes parelles de mots i, finalment, hom accepta el fet que, en substituir en un mot M = M 1 mM 2 un cert sumbmot m per un altre mot m´ equivalent, obté un mot equivalent M´ = M 1 m' M 2 Cal plantejar la pregunta següent donats dos mots arbitraris M i N , hi ha algun algorisme que permeti de decidir si…
relació d’equivalència
Matemàtiques
Relació binària entre els elements d’un conjunt que permet d’establir una classificació d’aquests elements de tal manera que resti cadascun en una classe, dita d’equivalència, i aquestes classes no tinguin cap element comú.
Perquè una relació sigui d’equivalència cal que sigui reflexiva, simètrica i transitiva relació Tota relació d’equivalència estableix una classificació del conjunt i tota classificació determina una relació d’equivalència Són equivalents dos elements que pertanyen a la mateixa classe El conjunt de les classes considerada cadascuna com un nou element és anomenat conjunt quocient del conjunt de partida C per a aquesta relació R , i s’escriu C/R Una aplicació d’un conjunt en un altre determina una relació d’equivalència entre els elements del conjunt original, prenent com a…
Jevgenij Slutskij
Economia
Matemàtiques
Economista i matemàtic rus.
Inicià la seva formació com a matemàtic a Kíev i enginyer a Munic s’interessà posteriorment per l’economia política i el dret Collaborà amb l’Institut Central de Meteorologia 1931-34 i des del 1934 amb l’Institut Matemàtic de l’Acadèmia de Ciències de l’URSS L’obra per la qual és més conegut és l’article sobre la teoria del comportament del consumidor 1915, en el qual estableix les relacions existents entre els preus, la renda i el consum i, en especial, la juxtaposició de l’efecte renda i l’efecte substitució, ocasionada per la modificació del preu d’un bé Aquesta acció…
teorema de Breusch
Matemàtiques
Teorema que estableix que per a qualsevol enter n ≥48, existeix un enter primer entre n i 9n|8.