Resultats de la cerca
Es mostren 22 resultats
àlgebra

Triàngle numèric, més tard conegut com a triangle de Pascal, d’un manuscrit xinès del 1303
© Fototeca.cat
Matemàtiques
Branca de les matemàtiques que estudia les estructures algèbriques dels conjunts.
Hom l’aplica, per tant, en les situacions on hi ha un conjunt ben definit i una noció clara d’operació entre els seus elements operació interna o entre aquests i els elements d’altres conjunts operació externa L’àlgebra ha evolucionat des de l’interès inicial per a resoldre problemes fonamentalment pràctics fins al desenvolupament del mètode abstracte Dues inclinacions diferents han desembocat en l’àlgebra moderna D’una banda, l’ àlgebra clàssica , simple instrument per a fer càlculs i resoldre equacions que usava només els conceptes immediats que hom reconeixia al problema les quantitats…
dependència algèbrica
Matemàtiques
Relació jeràrquica entre les estructures numèriques.
Per exemple, un subconjunt A del conjunt dels nombres complexos ℂdepèn algèbricament del conjunt dels nombres reals ℝ, si els seus elements poden ésser arrels d’un polinomi amb coeficients en ℝ anàlogament, una part de R pot dependre algèbricament de ℚ En ℝ, els nombres que no depenen algèbricament de ℚ, essent-ne doncs algèbricament independents, són anomenats nombres transcendents així doncs, els nombres transcendents, com e o π, no són arrels de cap polinomi amb coeficients en ℚ
àlgebra no commutativa
Matemàtiques
Part de l’àlgebra, entesa com a teoria de les estructures algèbriques, que estudia precisament aquelles estructures algèbriques en les quals l’operació fonamental no és pas commutativa.
Principalment es preocupa de la teoria de grups
isomorf | isomorfa
Matemàtiques
Dit de les estructures algèbriques entre les quals hom pot establir un isomorfisme.
immersió
Matemàtiques
Aplicació injectiva d’un conjunt A en un altre B, que conserva les estructures.
L’aplicació f és morfisme si A i B són espais topològics Tota immersió de A dins B permet d’identificar estructuralment A amb la seva imatge
lògica algèbrica
Matemàtiques
Estudi algèbric de la lògica com a llenguatge (metallenguatge).
La lògica algèbrica tracta, doncs, les estructures que presenten les diferents lògiques i d’aquesta manera arriba a trobar estructures algèbriques —poc usuals en l’àmbit de l’àlgebra clàssica— com són, entre d’altres, les àlgebres de Hilbert, de Heyting, d’Abbott, de Boole, de Wajsberg, monàdiques, poliàdiques i cilíndriques
taxonomia
Matemàtiques
Branca de les matemàtiques que estudia problemes de classificacions.
La teoria matemàtica de la taxonomia versa, doncs, sobre el tractament rigorós de les eines matemàtiques que comporta l’estudi de les classificacions, des de les estructures abstractes generadores de classificacions de diferents tipus com particions amb encavalcament preordres, particions equivalències, arbres ordres estratificats, jerarquies, similituds, etc, fins a mesures del “poder separador” de les classificacions índexs de distància i de similitud, estructures ultramètriques Tracta tant sobre els criteris com sobre els algorismes per a la descripció matemàtica…
homologia
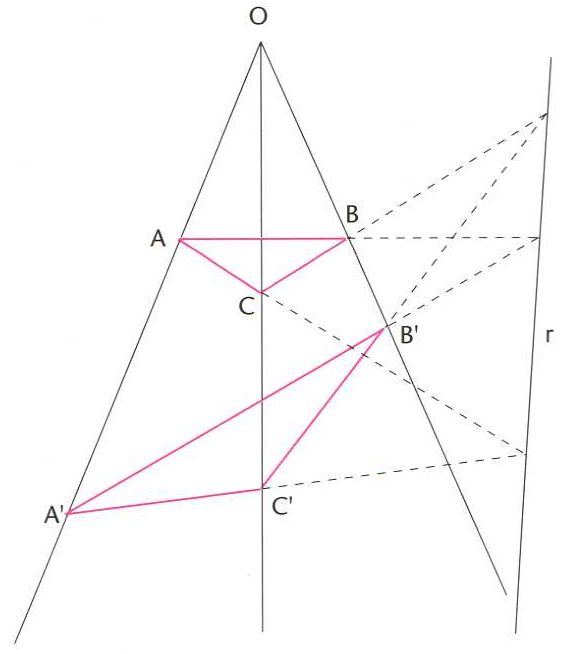
Trasformació per homologia d’un triangle ABC en A'B'C’ (O, centre de l’homologia; r, eix de l’homologia)
© Fototeca.cat
Matemàtiques
Teoria que estudia les transformacions entre espais topològics que conserven certes estructures algèbriques definides en cada espai.
desigualtat de Schwarz
Matemàtiques
Desigualtat enunciada per H.A. Schwarz, que es compleix en tot espai vectorial E dotat d’un producte escalar <, >, expressada per |<x,y>|2≤<x,x> <y,y>.
La igualtat es dóna només en el cas que x,y siguin linealment dependents y = a x , essent a un nombre Aquesta desigualtat és fonamental en l’estudi dels espais de Hilbert, estructures bàsiques de l’anàlisi funcional
estructura algèbrica
Matemàtiques
Conjunt en què hom ha definit una o unes quantes relacions binàries o lleis de composició.
Una llei de composició interna definida en un conjunt E és una operació que permet de fer correspondre a cadascun dels parells ordenats a, b d’elements, distints o no de E , un element ben determinat del mateix conjunt E Així, doncs, una llei de composició apareix com una aplicació de E × E en E Una estructura és definida, doncs, per mitjà d’un cert nombre d’axiomes que determinen les relacions i les operacions que la componen Les estructures més freqüents en àlgebra són les de grup, anell, cos i espai vectorial