Resultats de la cerca
Es mostren 20 resultats
extensió
Matemàtiques
Ampliació d’un conjunt o d’una estructura per afegiment de nous elements.
Hom construeix els successius conjunts numèrics per extensió
cos
Matemàtiques
Conjunt dotat de dues operacions, que hom acostuma a designar + i × (suma i producte), amb les següents propietats: respecte a la suma el conjunt té estructura de grup commutatiu, i també amb el producte és grup, commutatiu o no, i segons això el cos es dirà d’una manera o d’una altra.
A més, hom exigeix que l’operació × tingui la propietat distributiva respecte a la + Hom pot dir, doncs, que un cos és un anell tal, que cada element té invers respecte a l’operació × Un cos té només dos ideals el 0 i ell mateix Els exemples més immediats són el cos ℝdels nombres reals, amb les operacions usuals de suma i producte, el cos ℚdels nombres racionals i el ℂdels complexos Hi ha el cos de dos elements 0 i 1, amb les operacions + 0 element neutre 1 + 1 = 0, i × habitual Com a exemple de cos no commutatiu hi ha el dels quaternions La característica d’un cos és el nombre més petit p…
punt
Matemàtiques
Element de l’espai al qual hom no atribueix cap extensió, sinó solament posició.
àrea
Matemàtiques
Mesura o grandor de l’extensió o porció del pla ocupada per una figura.
La teoria elemental de les àrees dels polígons pren com a unitat d’àrea el quadrat que té per costat la unitat de longitud Un rectangle de costats de longitud entera conté tants quadrats unitat com indica el producte de les seves dimensions Si les mesures dels costats del rectangle són fraccionàries hon divideix els costats en parts iguals, tantes com indiquen els denominadors d’aquelles mesures Resulta sempre la mateixa regla hom obté l’àrea d’un rectangle multiplicant les seves dues dimensions Si les mesures dels costats són irracionals hom pren aproximacions per defecte i per excés L’àrea…
fórmula d’Heró
Matemàtiques
Fórmula per a calcular la superfície S d’un triangle a partir, únicament, dels seus costats a, b, c.
La fórmula és on p = 1/2 a+b+c és el semiperímetre del triangle L’extensió al cas del quadrilàter és la fórmula de Brahmagupta
quaternió
Matemàtiques
Símbol del tipus a +bi + cj +dk, on a, b, c, d són nombres reals i i, j, k segueixen les regles formals algèbriques: i2 = j2 = k2 = -1, i · j =-j · i =k, j k = -k . j = i, k . i =-i · k = j
.
Els quaternions poden ésser operats algèbricament suma i producte, com els complexos, dels quals són una extensió El conjunt dels quaternions té estructura de cos no commutatiu Els quaternions foren introduïts i estudiats per WRHamilton
teorema d’Hermite
Matemàtiques
Teorema que afirma que el nombre e és un nombre transcendent.
Fou demostrat per ChHermite el 1873 L’extensió del teorema, que afirma que per a qualsevol nombre algèbric α, el nombre e α és un nombre transcendent, és conegut com a teorema d’Hermite-Lindemann
funció logarítmica
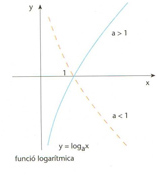
Funció logarítmica
© Fototeca.cat
Matemàtiques
Funció inversa de la funció exponencial
.
És anomenada també funció logaritme Si x = a y , on a > 0 i a ≠1, la funció logarítmica de base a fa l’assignació x → y ≡log a x Hom empra generalment la funció logarítmica de base 10 log 1 0 x i la que té per base el nombre e, o funció logaritme neperià L’extensió al cos ℂés la funció logarítmica complexa
Hermann Günther Grassmann
Lingüística i sociolingüística
Matemàtiques
Matemàtic i lingüista alemany.
Fou capdavanter de la moderna anàlisi vectorial i autor de diversos manuals d’aritmètica i de trigonometria entre altres, de Die Wissenschaft der extensiven Grössen oder die Ausdehnungslehre ‘La ciència de les magnituds extensives o la teoria de l’extensió’, 1844 i de Die Ausdehnungslehre 1862 i, com a lingüista, de Wörterbuch zum Rig-Veda ‘Diccionari del Rig-Veda’, 1875 i una traducció del Rig-Veda 1876-77
Haskell Brooks Curry
Lògica
Matemàtiques
Filosofia
Lògic i filòsof de la matemàtica nord-americà.
Professor de la Universitat de Pennsilvània 1941, fou el creador de la lògica combinatòria en sistematitzar la teoria esbossada per Schönfinkel durant el segon decenni del s XX L’estudi de les aplicacions d’aquests nous conceptes i l’extensió de llur camp d’acció constitueixen el material de Combinatory Logic 1958, escrita en collaboració amb Robert Feys Treballà també en els camps de la metalògica i la fonamentació de les matemàtiques, adscrit en tot a l’escola formalista