Resultats de la cerca
Es mostren 5 resultats
sistema de generadors
Matemàtiques
Subconjunt d’un grup G, d’un anell A, d’un espai vectorial E, etc, tal, que l’únic subgrup, subanell, subespai vectorial, etc, que el conté és total, és a dir, és el grup G, l’anell A, l’espai E, etc.
Posat que el sistema de generadors consti d’un sol element, aquest és anomenat generador del grup, de l’anell , etc
tor
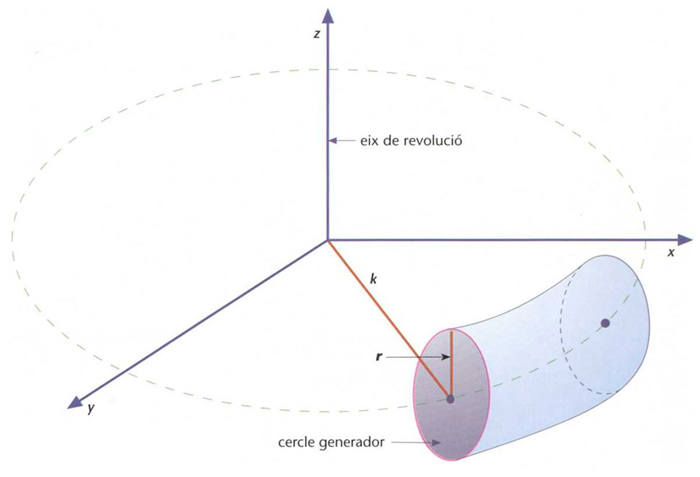
Generació d’un tor per un cercle
© Fototeca.cat
Matemàtiques
Superfície generada per la rotació, en l’espai, d’un cercle al voltant d’un eix del seu pla que no talla el cercle.
És la forma d’un anell de contorn circular i rodó Si r és el valor del radi del cercle generador, k la distància del centre a l’eix de revolució eix z , l’equació del tor és el seu volum val 2π kr, i l’àrea de la seva superfície, 4 π 2 kr
trocoide
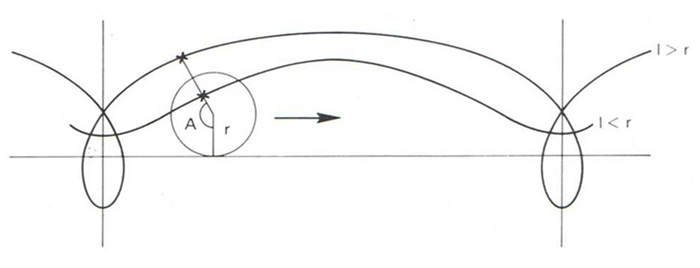
Trociode
© fototeca.cat
Matemàtiques
Corba descrita per un punt fixat a un cercle quan aquest cercle roda sense lliscament sobre una línia recta fixa.
Si el radi del cercle és r , la distància del punt generador al centre del cercle és l i A és l’angle determinat pel punt quan el cercle ha rodat A radiants, aleshores les equacions paramètriques de la trocoide són x = rA-l sin A y = r-l cos A Si l és major que r punt exterior al cercle, la trocoide descriu rulls si l és menor que r punt interior al cercle, la trocoide no toca mai la línia recta fixa base del desplaçament si el punt és el centre del cercle, la trocoide és una recta si l és igual a r punt de la circumferència, la trocoide és aleshores una cicloide
grup cíclic
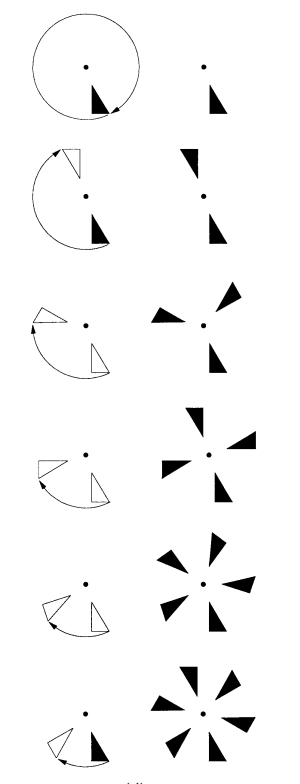
grups cíclics
© Fototeca.cat
Matemàtiques
Grup abelià G format per totes les potències enteres d’un element g, anomenat generador de G. Per exemple, el grup dels enters (ℤ, +) és un grup cíclic de generador el número 1.
grup
Matemàtiques
Estructura algèbrica constituïda per un conjunt G on hi ha definida una operació, designada per *, que per a qualssevol elements a, b, c de G té aquestes tres propietats: propietat associativa, o sia (a*b) *C = a*(b*c); G conté un element neutre e, o sia a*e = a; i per a qualsevol element a n’hi ha un altre de G, representat per a’, que és el seu invers (a*a’ = a’*a = e).
Si a més es compleix la propietat commutativa a*b = b*a , el grup és anomenat commutatiu o abelià i, en aquest cas, si hom representa l’operació amb el signe +, el grup és anomenat també additiu , mentre que si hom utilitza el signe o uns altres, el grup és anomenat també multiplicatiu Hom anomena ordre d’un grup el nombre d’elements que conté més exactament, és el cardinal del conjunt dels seus elements El grup és anomenat cíclic si qualsevol element s’obté per producte repetit d’un de fix, anomenat generador L’estudi en abstracte dels grups permet d’obtenir resultats aplicables a grups…