Resultats de la cerca
Es mostren 11 resultats
generatriu
generatriius
© Fototeca.cat
Matemàtiques
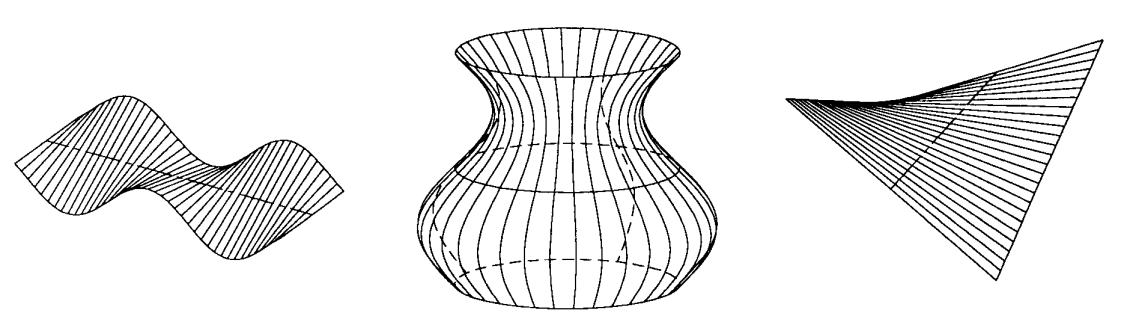
Punt, corba o superfície que, per mitjà d’un moviment subjecte a unes condicions determinades, genera una figura geomètrica.
Per exemple, un cilindre és generat per la rotació d’una recta la generatriu entorn d’un eix parallel a aquesta recta
funció generatriu d’un conjunt de funcions
Matemàtiques
Funció de dues variables f
( z,u
) tal que el seu desenvolupament en sèrie de potències respecte a una de les variables, p ex u
, té com a coeficients d’aquestes potències les funcions del conjunt en qüestió.
Així, la funció és la funció generatriu de les funcions de Bessel d’índex enter, J n z
superfície reglada
Superfícies reglades
Matemàtiques
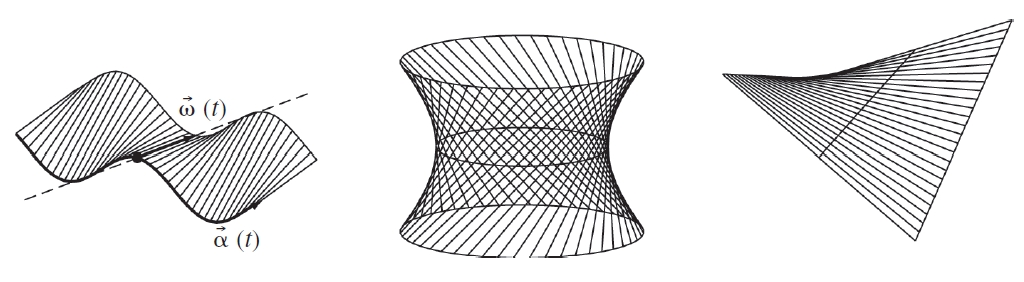
Superfície engendrada per una família infinita de rectes que depenen d’un paràmetre.
Cadascuna d’aquestes rectes és anomenada generatriu de la superfície els procediments habituals per a definir-les són donar les equacions d’una recta en l’espai amb un paràmetre variable, o bé donar tres corbes directrius i prendre com a generatrius les rectes que recolzen sobre aquestes tres corbes Hi ha dues classes de superfícies reglades si en tots els punts d’una mateixa generatriu la superfície té el mateix pla tangent, es tracta d’una superfície desenvolupable , i la superfície pot ésser construïda cargolant oportunament un o…
helicoide
Matemàtiques
Superfície generada per una semirecta R, l’extrem de la qual recorre una línia recta D, a la qual es manté sempre perpendicular, de manera que qualsevol punt fix M de la semirecta descriu una hèlix que té R per eix.
La semirecta R és la generatriu de l’helicoide
con
Matemàtiques
Superfície reglada generada per totes les rectes (generatrius) que passen per un punt dit vèrtex i per una corba (exterior al punt donat) dita directriu.
La superfície consta de dos fulls units pel vèrtex Es parla de con de revolució si la superfície cònica és engendrada per una recta que passa pel vèrtex i gira al voltant d’una altra recta que també hi passa, la qual és anomenada eix del con Les corbes obtingudes en tallar un con de revolució amb un pla que no passa pel vèrtex reben el nom de seccions còniques o, simplement, còniques Si el pla secant és parallel a una generatriu del con, la cònica rep el nom de paràbola en la resta de casos, el pla secant determina una ellipse o una hipèrbola, segons si el pla talla un full…
con
con
© Fototeca.cat
Matemàtiques
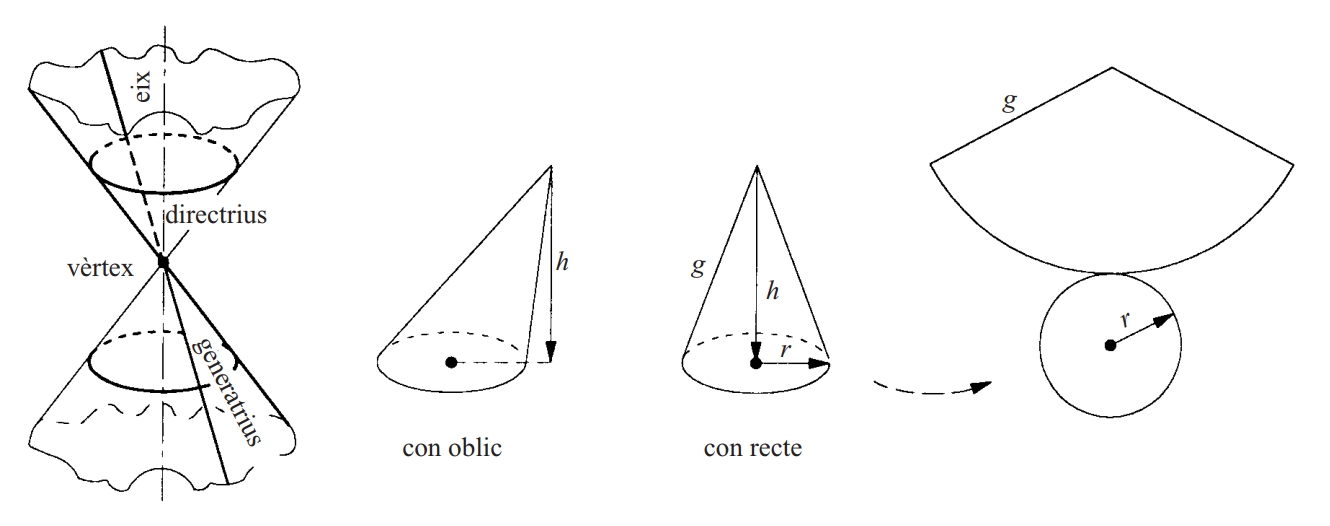
Cos limitat per un pla que conté una corba tancada (base del con) i pel conjunt de semirectes que, partint d’un punt fix (vèrtex del con) exterior al pla de la base, recolzen sobre la corba.
Es parla de con circula r si la base és una circumferència En un con circular, si la projecció del vèrtex sobre el pla de la base coincideix amb el centre, es parla de con recte , en cas contrari es parla de con oblic Els segments que tenen per extrems el vèrtex i un punt qualsevol de la base s’anomenen generatrius l’altura d’un con és la distància del vèrtex al pla de la base El volum d’un con és un terç de l’àrea de la base per l’altura L’àrea lateral d’un con circular recte és π rg , essent r el radi de la base i g la longitud de la generatriu
superfície de revolució
Superfície de revolució
Matemàtiques
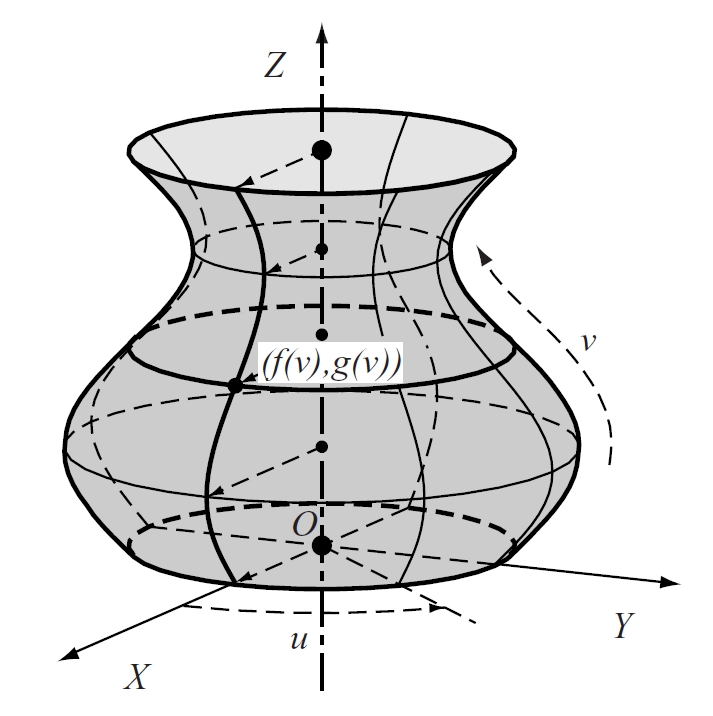
Superfície engendrada per la rotació d’una corba (generatriu) entorn d’un eix, anomenat de revolució.
Si aquesta corba és plana i situada en un pla que conté l’eix és anomenada meridiana de la superfície La circumferència descrita per cada punt de la meridiana és anomenada parallel Els meridians i els parallels d’una superfície esfèrica són circumferències Els meridians de la superfície terrestre són aproximadament ellipses
oblic | obliqua
Matemàtiques
Dit del cilindre determinat per la intersecció d’una superfície cilíndrica amb dos plans no perpendiculars a la generatriu de la superfície.
hipèrbole
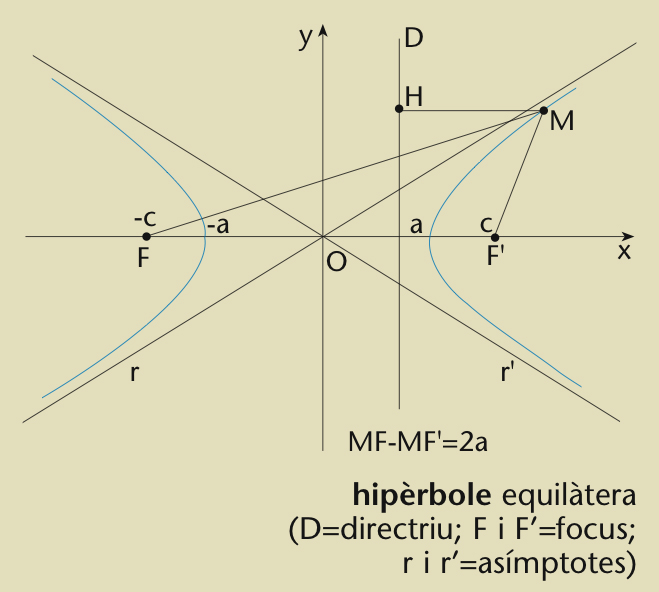
Hipèrbole equilàtera
© Fototeca.cat
Matemàtiques
Corba oberta, intersecció d’un con de revolució amb un pla que forma amb ’eix d’aquell un angle més petit que amb la generatriu.
Constitueix el lloc geomètric dels punts del pla tals que la diferència de llurs distàncies a dos punts fixos, anomenats focus , és una constant, simbolitzada habitualment per 2 a Té dos eixos de simetria i, referida a ells, la seva equació és x 2 / a 2 - y 2 / b 2 = 1, on i 2c és la distància entre els focus L’excentricitat e és c / a Les asímptotes són les rectes y = b / a x asímptota Quan a = b , la hipèrbola és anomenada equilàtera , i la seva equació referida a les asímptotes, que són perpendiculars, és y = k/ x la seva excentricitat és
superfície cilíndrica
Matemàtiques
Superfície engendrada per una recta (generatriu) que es mou paral·lelament a un eix fix, recolzant en una corba plana (directriu) el pla de la qual talla l’eix.