Resultats de la cerca
Es mostren 6 resultats
base d’un mòdul
Matemàtiques
Conjunt linealment independent d’elements del mòdul
que el generen mitjançant combinacions lineals.
mosaic
mosaics
© Fototeca.cat
Matemàtiques
Recobriment del pla per repetició d’un mòdul fix segons dues direccions.
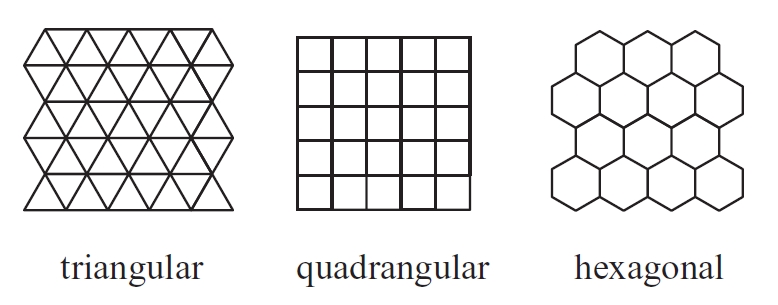
Els mosaics regulars s’obtenen per repetició d’un polígon regular Els mosaics semiregulars es generen en combinar dos tipus de polígons regulars de dimensions convenients per al seu acoblament Únicament hi ha tres tipus de mosaics regulars i vuit de semiregulars Els únics mosaics regulars que es poden construir al pla són el triangular, el quadrangular i l’hexagonal
teoremes de Guldin
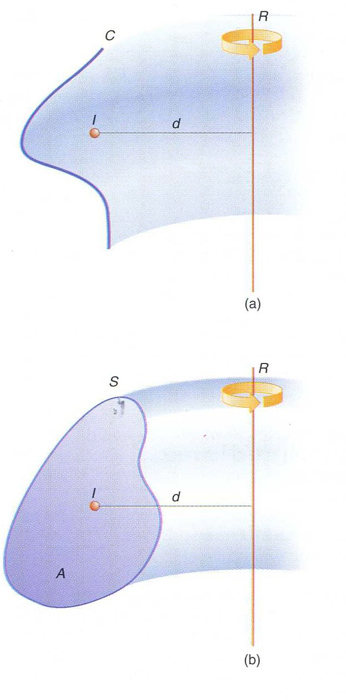
teoremes de Guldin: (a) primer teorema; (b) segon teorema
© fototeca.cat
Matemàtiques
Teoremes que relacionen el centre de massa d’una corba o d’una superfície amb l’àrea o el volum, respectivament, que generen en girar al voltant d’un eix.
Segons el primer teorema de Guldin , donada una corba plana C , de longitud l , que gira al voltant d’una recta R del seu pla, la qual no talla, l’àrea A de la superfície de revolució que genera és A = 2π dl , on d és la distància des del centre de massa I de la corba a la recta R en el cas purament geomètric, el centre de massa és calculat assignant la mateixa “massa” a tots els punts de la corba matemàtica en el cas físic, el centre de massa és el del sistema de masses puntuals de la corba material El segon teorema de Guldin afirma que, donada una superfície plana S , d’àrea A , que gira al…
mètode de racionalització de Gauss
Matemàtiques
Algorisme emprat en l’estudi dels espais vectorials que, donats uns vectors arbitraris, permet de deduir-ne efectivament els que són linealment independents i que, per tant, també són base del subespai que generen.
Hom aplica aquest mètode per a trobar el rang d’una matriu qualsevol no necessàriament quadrada, considerant cada fila de la matriu com un vector
base d’un espai vectorial
Matemàtiques
Conjunt de vectors linealment independents que generen l’espai vectorial mitjançant combinacions lineals, és a dir, tals que qualsevol vector v de l’espai pot ésser expressat d’una manera unívoca com a combinació lineal dels vectors de la base:
Les coordenades a 1 ,, a n de v en la base e 1 ,, e n són úniques Tot espai vectorial té una base és una conseqüència de l’axioma de Zermelo Si l’espai E té una base formada per un nombre finit d’elements base finita l’espai és de dimensió finita aleshores totes les bases tenen el mateix nombre d’elements, nombre que s’anomena la dimensió de l’espai , dim E Un espai vectorial de dimensió finita té infinites bases Dues bases de E , B = e 1 ,, e n i B’ = e’ 1 ,, e’ n es relacionen mitjançant una matriu de canvi de base essent és a dir, les matrius A i B són inverses B = A -1 La matriu…
espai vectorial
Matemàtiques
Grup abelià E
en el qual hi ha definida una llei de composició externa amb elements d’un cos K
, K
× E
→ E tal, que al parell (λ, e
) correspon l’element λ e
.
I acomplint-se les propietats λ + μ e = λ e + μ e , λ e + f = λ e + λ f , λμ e = λμ e i 1 e = e Els elements de E són anomenats vectors , i els elements de K , escalars Una part de E que sigui subgrup respecte a la suma i que sigui estable respecte al producte per qualsevol escalar, és anomenada subespai de E , i amb les mateixes operacions de E és un altre espai vectorial Si F és un subespai de E , hom pot definir congruències a E mitjançant la relació d’equivalència x ≡ y mòd F , si i només si la diferència x — y pertany a F Això permet de formar el conjunt quocient E/F quocient, el…