Resultats de la cerca
Es mostren 13 resultats
funció multiforme
Matemàtiques
Funció que assigna diverses imatges a cada element del domini de definició.
En són exemple les funcions trigonomètriques inverses arc sin1 = {π/2, π/2+2π, π/2+4π,,π/2+2 n π,} Les funcions multiformes no són, en el sentit estricte del terme funcions , sinó correspondències Una funció multiforme esdevé una funció quan hom n'escull una branca o determinació per exemple, la funció Arc sin x és la branca de la funció multiforme arc sin x definida en restringir a 0,2π el recorregut d’aquesta
aplicació
fototeca.cat
©
Matemàtiques
correspondència
entre dos conjunts en què tot element del primer conjunt (o original) té una imatge i una de sola en el segon conjunt.
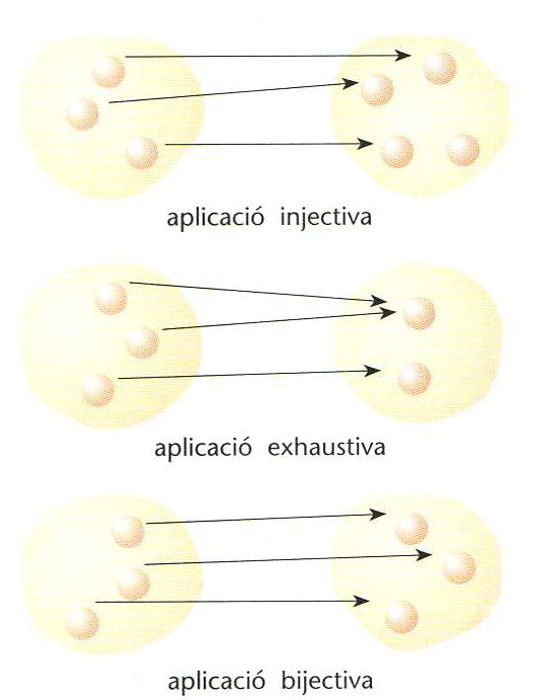
Si elements diferents tenen imatges diferents, l’aplicació és dita injectiva si tot element del segon conjunt és imatge d’un element almenys del primer, l’aplicació és exhaustiva una aplicació que sigui alhora injectiva i exhaustiva és dita bijectiva o unívoca
base dual
Matemàtiques
Base definida en un espai vectorial E de dimensió finita.
Si e 1 , e n és una base de E , aleshores el conjunt de formes lineals f i E→K, amb imatges sobre el cos K de l’espai vectorial, definits per f i e j =δ i j , essent δ i j =0 si i ≠ j , δ ij =1, forma una base de l’espai dual E *, i s’anomena la base dual de la inicial
Vicent Caselles i Costa
Matemàtiques
Matemàtic.
Llicenciat per la Universitat de València, amplià estudis a les universitats de Tübingen i Besançon Professor, successivament, a la Universitat de les Illes Balears 1994 i a la Universitat Pompeu Fabra 1999, d’on esdevingué catedràtic el 2002, és autor d’uns 200 treballs publicats que el convertiren en el matemàtic de l’Estat espanyol més citat internacionalment Inicialment, es dedicà a l’anàlisi funcional i, posteriorment, al processament digital d’imatges i el seu tractament per ordinador, matèries en les quals esdevingué un referent internacional De les seves publicacions hom…
funció
Matemàtiques
Aplicació.
Segons els casos, hom fa ús d’un o de l’altre dels dos sinònims, funció o aplicació així, hom parla d’aplicació entre conjunts no numèrics o d’aplicació injectiva, però de funció entre conjunts numèrics o de funció derivable El concepte de funció és un dels conceptes fonamentals de la matemàtica Una funció entre dos conjunts A i B és representada per la notació fA →B A és el domini de definició o el camp d’existència de f , i el subconjunt de B format per les imatges dels elements de A , denotat per f A , és la imatge , abast, rang o recorregut de f Si x representa un element…
homologia
Matemàtiques
Transformació geomètrica del pla o de l’espai tal que cada punt i la seva imatge són alineats amb un punt fix anomenat centre d’homologia, i si tres punts són alineats, llurs imatges també ho són.
morfisme
Matemàtiques
Aplicació f entre dos conjunts A i B dotats d’estructura algèbrica, que conserva les operacions en el sentit que operar dos elements del conjunt A i cercar la imatge del resultat coincideix amb el fet d’operar les respectives imatges.
Així, per exemple, un morfisme d’anells, f A → B , definit per l’assignació x → f x , compleix les relacions f x + y = f x + f y i f xy = f x f y En el cas que un morfisme és a dir, l’aplicació f sigui injectiu , exhaustiu o bijectiu aplicació 3, és anomenat, respectivament, monomorfisme , epimorfisme o isomorfisme D’altra banda, un morfisme entre un conjunt i ell mateix és anomenat endomorfisme, i si és un isomorfisme, aleshores és anomenat automorfisme Els morfismes, en general, són anomenats també homomorfismes , i els morfismes entre espais vectorials, els quals tenen un…
semblança
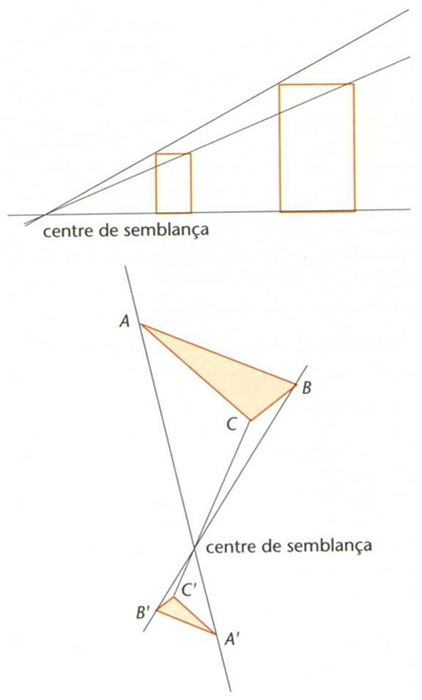
Dues semblances directes
© Fototeca.cat
Matemàtiques
Transformació geomètrica T de ℝn en ℝn tal que la distància entre les imatges de dos punts qualssevol és igual a la distància entre aquests dos punts multiplicada per una quantitat constant positiva dita raó de la semblança.
És a dir, d T x, T y = k, d x, y Dues figures són anomenades semblants si hi ha una semblança que transforma l’una en l’altra Les semblances conserven la forma de les figures però en canvien la grandària, eixamplant-la o reduint-la segons que la raó sigui respectivament major o menor que 1 Les semblances de raó 1 són dites isometries o moviments rígids , els quals són sempre el resultat de compondre una translació amb una transformació lineal ortogonal que conserva els angles Les homotècies són exemples típics de semblances Tota semblança és el resultat d’aplicar successivament una…