Resultats de la cerca
Es mostren 29 resultats
desigualtat
Matemàtiques
Donada una relació d'ordre en un conjunt C, expressió que indica la relació entre dos elements determinats.
L’expressió a < b és una desigualtat entre a i b , i es llegeix ''a és inferior a b' o '' a és anterior a b ' l’expressió a > b es llegeix ''a és superior a b' o '' a és posterior a b ' Amb l’expressió a ≥b hom indica que ''a és inferior o igual a b’ i amb a ≤b que '' a és posterior o igual a b' Quan C és un conjunt numèric, les expressions a b, a ≤b i a ≥b indiquen, respectivament, que a és menor, major, menor o igual o major o igual, que b
igualtat i desigualtat de Bessel
Matemàtiques
Expressions que se satisfan per a tot element x d’un espai prehilbertià, del qual x1,...,xnsón un conjunt de vectors ortonormals.
La igualtat de Bessel és l’expressió on x|x k indica el producte escalar de x i x k , i ∥ x ∥indica la norma del vector x Hom en dedueix la desigualtat de Bessel
base d’una potència
Matemàtiques
Factor que cal multiplicar per ell mateix tantes vegades com indica l’exponent.
radical
Matemàtiques
Signe √ emprat per a indicar l’arrel enèsima d’una quantitat o expressió.
Hom hi indica, a més, l’índex n de l’arrel, llevat del cas en què n = 2, és a dir, en el cas de l’arrel quadrada arrel
àlef
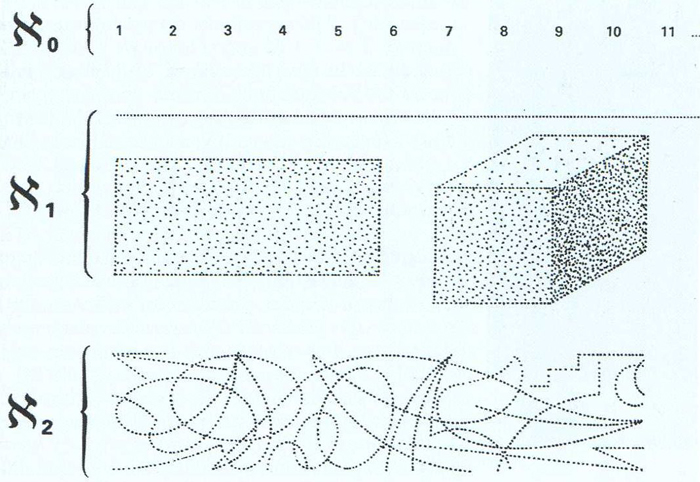
Comparació del cardinal dels naturals, ℵ0, amb els cardinals estrictament més grans: ℵ1, cardinal del continu, i ℵ2, cardinal de les corbes del pla
© Fototeca.cat
Escriptura i paleografia
Matemàtiques
Símbol ℵ que designa el cardinal dels conjunts infinits ben ordenats.
Acompanyat pel subíndex zero indica la classe dels conjunts infinits numerables, que permeten d’establir una correspondència biunívoca amb els nombres naturals, 1, 2, 3, Per exemple, el conjunt dels nombres parells té cardinal, ja que a cada nombre parell 2n hom pot fer correspondre la seva meitat n
autòmat finit determinista
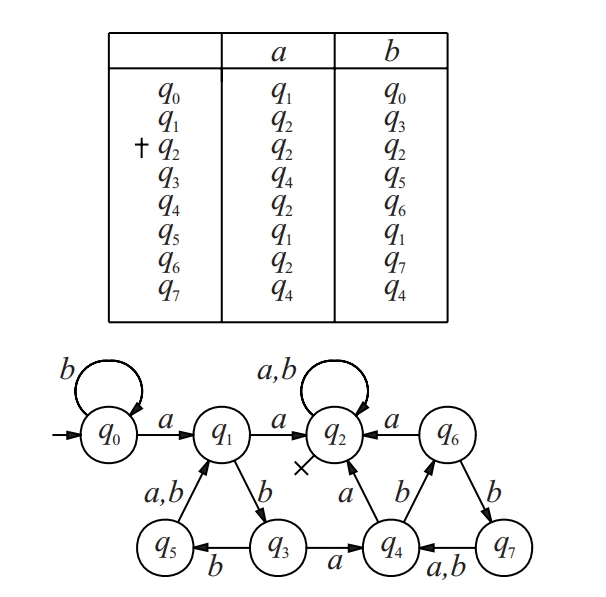
autòmat finit determinista
Matemàtiques
Estructura de la forma M = (Q, ∑, δ, q0, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet, anomenat d’entrada; δ : Q ⨉ ∑* → Q és la funció de transició que satisfà ∀q ∈ Q, ∀x,y ∈ ∑*:δ(q, λ) = q, δ(q, xy) = δ(δ(q, x), y) essent xy la concatenació de x i de y, i λ la paraula buida i ∑* el conjunt de paraules; q0 ∈Q s’anomena estat inicial; F ⊂ Q s’anomena conjunt d’estats finals o acceptadors.
Usualment un autòmat finit determinista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si δ q i , a = q j S’indica l’estat inicial amb una fletxa i els finals amb una creu
co-
Astronomia
Matemàtiques
Prefix llatí que indica el complement d’un angle o la pertinença a aquest complement.
projecció fitada
Matemàtiques
Sistema de projecció que utilitza només com a pla de projecció el pla horitzontal i substitueix el vertical per un nombre.
Aquest nombre, que indica la distància del punt al pla, és escrit al costat de la projecció horitzontal en una unitat determinada El pla de projecció rep el nom de pla de comparació i els nombres escrits amb cada projecció són anomenats fites Així, un punt és determinat per la seva situació a l’espai respecte al pla de comparació i la seva fita Per distingir els punts que hi ha a sobre del pla de comparació dels que hi ha a sota, els primers porten la fita positiva i els segons negativa
Pedro Nunes
Astronomia
Matemàtiques
Astrònom i matemàtic portuguès.
Conegut també amb el nom llatinitzat de Petrus Nonius , inventà el doble regle graduat, capaç d’apreciar fraccions de longitud inferiors al mig millímetre nònius Cosmògraf reial i professor a Coïmbra, escriví De arte atque ratione navigandi 1546, on indicà que la distància mínima entre dos punts de la superfície terrestre no és donada per la corba que talla els meridians amb un angle constant, sinó per l’arc de cercle màxim És autor, també, d’un tractat d’àlgebra i donà la solució correcta al problema del crepuscle més curt
Joseph-Louis Lagrange
Matemàtiques
Matemàtic francès.
Continuador de l’obra d’Euler, fou cridat a Prússia per Frederic el Gran Traslladat definitivament a París el 1787, posà de manifest a l’École Polytechnique els seus amplis coneixements estudiant les equacions de grau superior al quart, indicà les bases de la futura teoria de grups Ideà el mètode d' interpolació que duu el seu nom És autor de Mécanique analytique 1788, Traité de la résolution des équations numériques 1798 i Leçons sur le calcul des fonctions 1799 La seva obra completa fou publicada a París del 1867 al 1892