Resultats de la cerca
Es mostren 7 resultats
lleis de De Morgan
Lògica
Matemàtiques
En lògica d’enunciats, lleis donades per les equivalències següents: no(P i Q) = (no P) o (no Q), i no(P o Q) = (no P) i (no Q).
En teoria de conjunts, lleis donades per les igualtats i on les barreres indiquen els conjunts complementaris Les lleis de De Morgan se satisfan en tota Boole, àlgebra de
fórmula de Bayes
Matemàtiques
Fórmula que permet de calcular, donades les probabilitats a priori P (Ai) corresponents a diverses causes A1,..., An, mútuament excloents, les probabilitats a posteriori P (Ai/B).
Aquestes probabilitats a posteriori o condicionades indiquen el fet que la causa A i hagi estat precisament la que ha motivat l’efecte B observat Té com a expressió La impossibilitat de conèixer en molts casos les probabilitats a priori és una limitació pràctica de l’aplicació de la fórmula
gràfic de control
Matemàtiques
Representació cronològica d’observacions relatives a mostres tretes d’un procés industrial per tal de controlar les característiques del producte i corregir, si cal, el funcionament del procés.
En el gràfic de control hom representa, generalment, les mitjanes i les amplituds diferència entre el valor més gran i el més petit de la mostra de les mostres El sistema de referència és constituït per uns eixos de coordenades i unes rectes horitzontals o límits que indiquen la necessitat d’extreure una mostra complementària límit d’atenció o bé d’intervenir directament en el procés per tal de corregir-lo límit d’intervenció
autòmat finit indeterminista
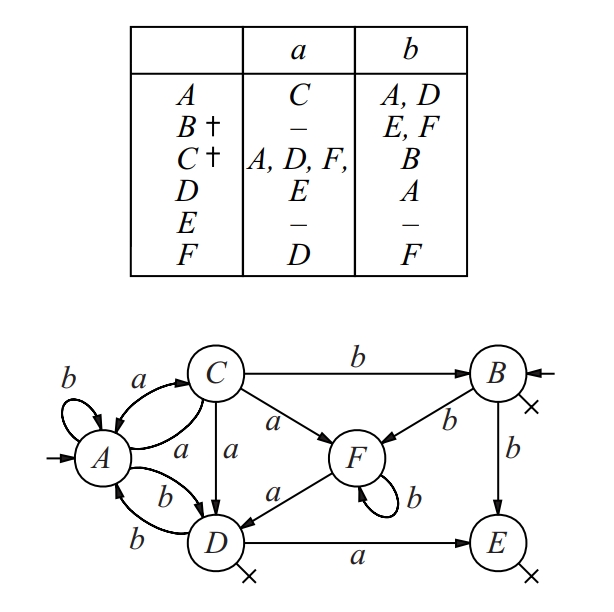
autòmat finit indeterminista
Matemàtiques
Estructura de la forma M = (Q, ∑, δ, I, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet anomenat d’entrada; δ : 2Q ⨉ ∑* → 2Q és la funció de transició que satisfà ∀P1, P2 ⊂ Q, ∀x, y∈∑*: δ(∅, x) = ∅, δ(P1, λ) = P1, δ(P1 ∪ P2, x) = δ(P1, x) ∪ δ(P2, x), δ(P1, xy) = δ(δ(P1, x)y), essent xy la concatenació de x i de y i ∑* el conjunt de paraules; I ⊂ Q és el conjunt d’estats inicial; F ⊂ Q és el conjunt d’estats finals o acceptadors.
Usualment un autòmat finit indeterminista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si q j ∈ δ q i , a S’indiquen els esstats inicials amb fletxes i els finals amb una creu Els llenguatges acceptats pels autòmats finits indeterministes són els mateixos que els reconeguts pels finits deterministes regulars L’avantatge dels indeterministes enfront dels deterministes és la facilitat de maneig i de construcció
desigualtat
Matemàtiques
Donada una relació d'ordre en un conjunt C, expressió que indica la relació entre dos elements determinats.
L’expressió a < b és una desigualtat entre a i b , i es llegeix ''a és inferior a b' o '' a és anterior a b ' l’expressió a > b es llegeix ''a és superior a b' o '' a és posterior a b ' Amb l’expressió a ≥b hom indica que ''a és inferior o igual a b’ i amb a ≤b que '' a és posterior o igual a b' Quan C és un conjunt numèric, les expressions a b, a ≤b i a ≥b indiquen, respectivament, que a és menor, major, menor o igual o major o igual, que b
osculador | osculadora
Matemàtiques
Dit de la corba o la superfície que, en un punt determinat, té el major contacte possible amb una altra corba o superfície.
Matemàticament, el pla osculador d’una corba guerxa és definit com el pla que adopta la posició límit dels plans determinats per tres punts veïns de la corba quan dos d’ells tendeixen a l’altre Si r = r t és l’equació paramètrica de la corba, l’equació del pla osculador en el punt r - r t 0 × r ´ t 0 r ´´ t 0 = 0, on les primes indiquen derivades temporals En les corbes planes, el pla osculador es redueix al pla de la corba L' esfera osculadora d’una corba guerxa és definida com l’esfera que adopta la posició límit de les esferes determinades per quatre punts de la corba…
àrea
Matemàtiques
Mesura o grandor de l’extensió o porció del pla ocupada per una figura.
La teoria elemental de les àrees dels polígons pren com a unitat d’àrea el quadrat que té per costat la unitat de longitud Un rectangle de costats de longitud entera conté tants quadrats unitat com indica el producte de les seves dimensions Si les mesures dels costats del rectangle són fraccionàries hon divideix els costats en parts iguals, tantes com indiquen els denominadors d’aquelles mesures Resulta sempre la mateixa regla hom obté l’àrea d’un rectangle multiplicant les seves dues dimensions Si les mesures dels costats són irracionals hom pren aproximacions per defecte i per…