Resultats de la cerca
Es mostren 6 resultats
cicloide
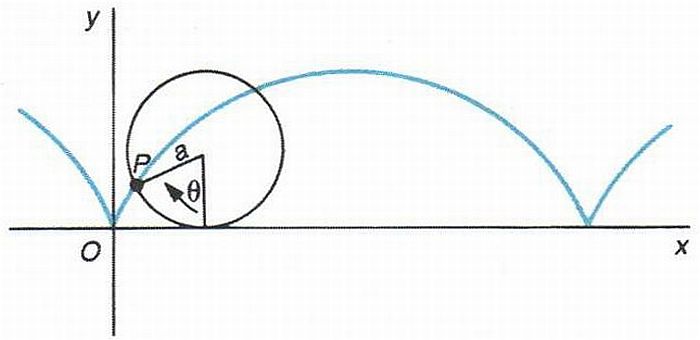
Cicloide
©
Matemàtiques
Corba engendrada per un punt fix en una circumferència que rodola, sense lliscar, damunt una recta.
Les seves equacions paramètriques són x = a θ - sinθ, y = a 1 - cosθ Hom pot ampliar aquesta definició considerant una trajectòria fixa en lloc d’una recta així, per exemple, l' epicicloide és la corba engendrada per un punt fix en una circumferència que rodola, sense lliscar, damunt una altra circumferència i exteriorment a ella
cardioide
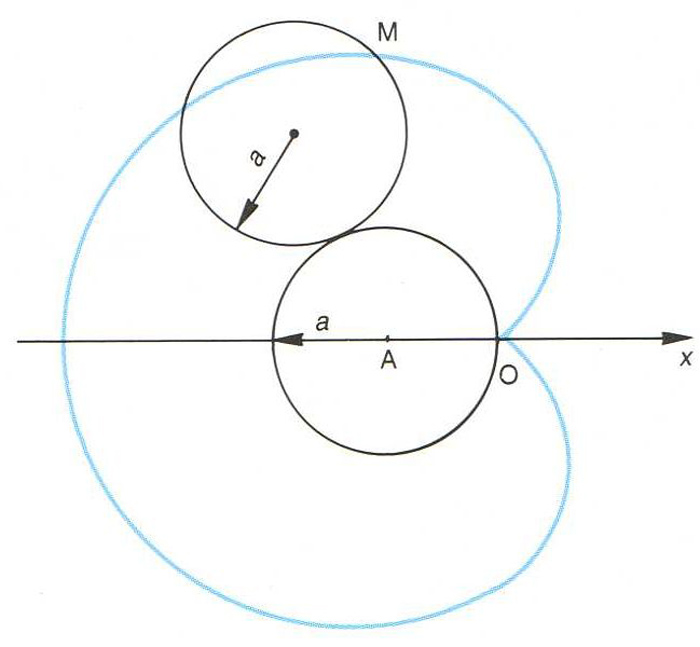
Cardioide determinada pel punt fix M d’un cercle de radi a que roda sense lliscar sobre un cercle fix de radi a i centre A. O és el punt de retrocés
© fototeca.cat
Matemàtiques
Epicicloide singular engendrada per les posicions d’un punt d’un cercle de radi a que roda sense lliscar per damunt d’un altre cercle del mateix radi.
Té un punt de retrocés O , respecte al qual l’equació de la cardioide en coordenades polars és ρ = 2 a 1-cos θ La longitud de la cardioide és aleshores 16 a i l’àrea és 6π a 2
nefroide
Matemàtiques
Epicicloide amb r = 2a
.
És generada per un cercle de radi a que rodola sense lliscar per l’exterior d’un cercle de radi 2 a Té una longitud de 24 a i una àrea de 12 π a 2
deltoide
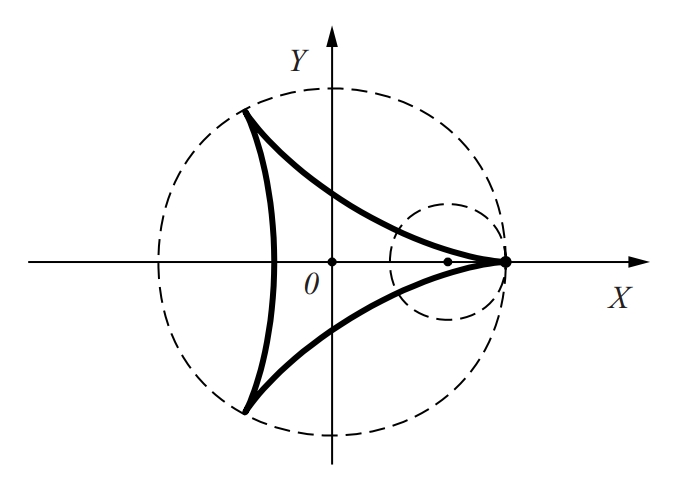
deltoide
Matemàtiques
Hipocicloide d’un cercle de radi k que roda, sense lliscar, dintre d’un altre que té el radi triple.
Les seves equacions paramètriques són x = k 2cos t + cos 2t , i y = k 2sin t + sin 2 t
epicicloide
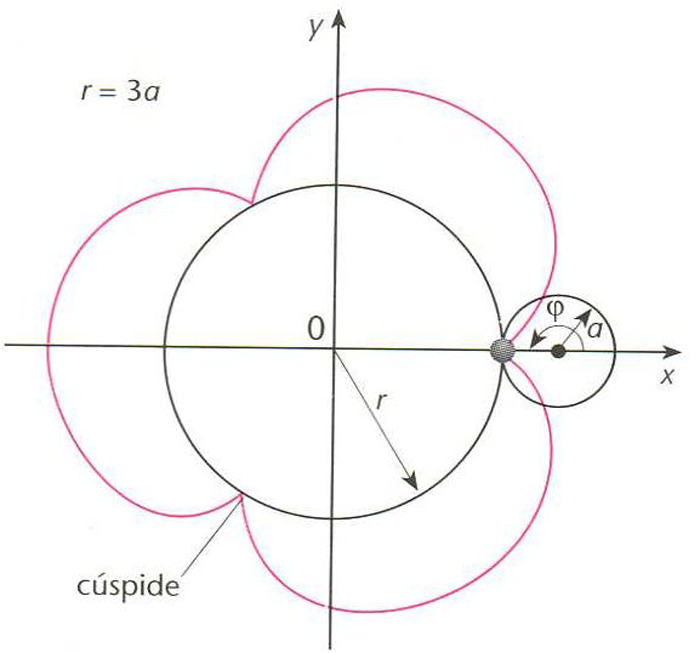
Epiciloide
© fototeca.cat
Matemàtiques
Corba descrita per un punt d’una circumferència que roda sense lliscar sobre una altra, mantenint-se tangents exteriorment ( cicloide
).
La seva equació és on r és el radi de la circumferència fixa, i a , el radi de la circumferència mòbil Si r = na , l’epicidoide té n cúspides n , nombre natural Si r = a la corba degenera en una cardioide Si r= 2 a , ho fa en una nefroide
hipocicloide
Matemàtiques
Corba engendrada per un punt fix d’una circumferència que roda, sense lliscar, per dins d’una altra, mantenint-se ambdues tangents interiors.
La seva equació és on r és el radi de la circumferència fixa, i a , el radi de la circumferència mòbil L’equació s’obté, doncs, de la de l'epicicloide fen a negativa Quan r= 3 a és una deltoide i quan r= 4 a és una astroide