Resultats de la cerca
Es mostren 39 resultats
recta real
Matemàtiques
Conjunt de tots els nombres reals, juntament amb llur representació en una recta graduada.
Cada representació resta fixada quan damunt una recta gràfica hom ha escollit un origen imatge del nombre zero i una unitat imatge del nombre u Sovint és utilitzat el llenguatge geomètric en parlar dels nombres reals el nombre x és en un entorn del nombre a
recíproca
Matemàtiques
Donada una quantitat a, la quantitat 1/a
.
És anomenada també inversa Les quantitats a i 1/ a són anomenades quantitats recíproques o inverses i llur producte és igual a 1
biaix d’ordenació
Matemàtiques
Electrònica i informàtica
Predisposició d’una distribució o seqüència a apartar-se de l’ordenació que fóra esperable si la distribució o seqüència es presentés realment a l’atzar.
Així, un inventari de documents que ha estat classificat per anys mostrarà un biaix a favor de l’ordenació cronològica és a dir, segons llur data
parell de nombres primers bessons
Matemàtiques
Parell (p,q) de nombres primers, en el qual q=p+2, p ex (5,7), (17,19).
Hom desconeix si llur nombre total és finit, però si sabem que la sèrie , on p recorre els nombres primers bessons, és convergent teorema de Brun
afinitat
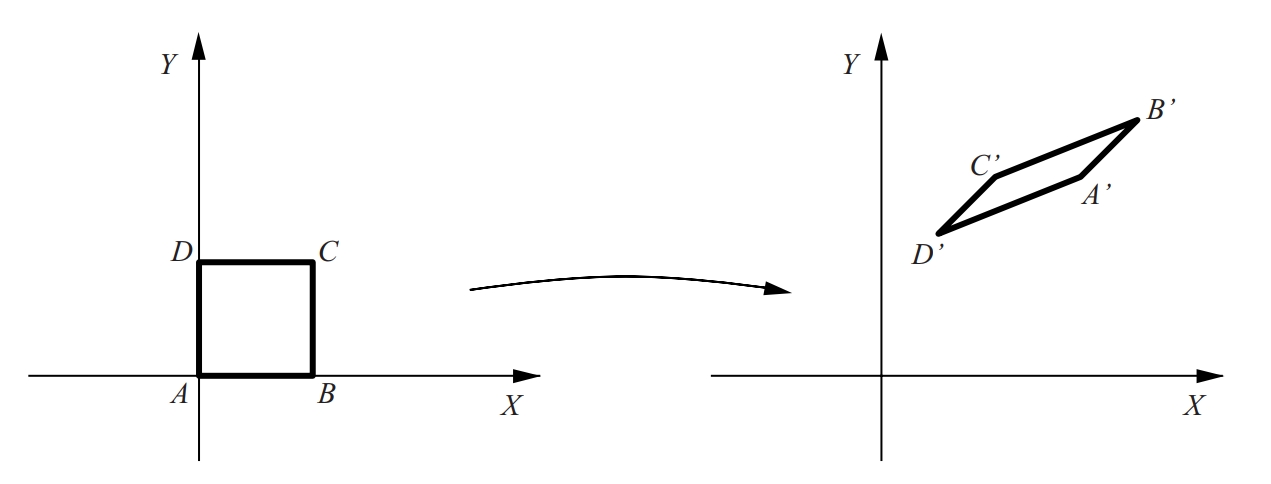
afinitat Transformació afí d’un quadrat
© Fototeca.cat
Matemàtiques
Transformació de l’espai afí en si mateix, que fa correspondre línies paral·leles amb línies paral·leles, punts propis amb punts propis i no canvia el subespai de l’infinit.
Enclou, entre d’altres transformacions, la traslació, la rotació i la simetria Les propietats geomètriques conservades per aquesta transformació són dites afins o lineals llur estudi constitueix la geometria afí
trapezi
Matemàtiques
Quadrilàter que té dos costats oposats paral·lels i els altres dos no paral·lels.
Els dos costats parallels b 1 i b 2 són les bases , i llur distància h és l' altura del trapezi L’àrea és h b 1 + b 2 /2, és a dir, el producte de l’altura per la semisuma de les bases Si els costats no parallels són iguals, és anomenat trapezi isòsceles
atzar
Matemàtiques
Conjunt de causes inconegudes que produeixen un efecte no previsible; un fenomen és atribuïble a l’atzar, o és fortuït o és aleatori, quan no és ni inevitable ni impossible.
Una característica important d’aquests fenòmens és que llur realització depèn d’un conjunt de condicions massa complexes per a poder-les conèixer i estudiar totes Un esdeveniment que apareix inevitablement quan es produeix un conjunt de condicions és un esdeveniment cert respecte a aquestes hom anomena impossibles els que mai no poden aparèixer Els esdeveniments fortuïts són els que tant poden donar-se com no donar-se si es realitzen les condicions és a dir, si aquestes no reflecteixen del tot les condicions necessàries i suficients perquè es realitzi l’esdeveniment, i es tracta…
relació binària
Matemàtiques
Condició relativa a dos elements d’un conjunt que és satisfeta per determinats parells d’elements (eventualment per tots o per cap parell).
Sovint hom representa una relació binària per una taula de doble entrada on són assenyalats els quadres corresponents als parells que satisfan la relació La taula següent dóna la relació a és múltiple de b entre els nombres del conjunt 1,2,3,4,5,6 Entre les relacions binàries sobresurten per llur importància les relacions d’equivalència i les relacions d’ordre
histograma
Matemàtiques
Representació gràfica, formada per rectangles, de les freqüències d’una variable.
Quan la variable pren valors discrets, tots els rectangles tenen la mateixa amplada i llur altura és proporcional a la freqüència corresponent al punt on el rectangle és situat Quan la variable és contínua, els rectangles són contigus i l’àrea de cadascun d’ells, que té per base un cert interval de la variable, és proporcional al valor global de la freqüència corresponent a l’interval
àbac

Àbac xinès
© Fototeca.cat
Matemàtiques
Aparell simple de càlcul digital que permet de fer totes les operacions aritmètiques bàsiques.
Consisteix, normalment, en un tauler o marc proveït de filferros parallels, amb boles foradades que corren al llarg d’aquests Cada enfilall representa un lloc decimal unitats, desenes, centenes, etc, i llur nombre pot ésser variable Les operacions s’efectuen canviant de posició unes boles en relació amb les altres, i, amb una manipulació complicada, hom pot aconseguir fins l’extracció d’arrels L’àbac fou usat a l’antic Egipte i probablement a Babilònia, d’on passà a Grècia i a Roma L’àbac romà consistia en una taula amb diverses ranures paralleles per on hom feia córrer pedres o botons, amb…