Resultats de la cerca
Es mostren 16 resultats
regressió
Matemàtiques
Estudi de la millor aproximació d’una variable estadística y a partir d’una família donada de variables estadístiques x1..., xn, mitjançant combinacions lineals del tipus a1 x1..., an xn + b, i prenent com a criteri de “millor aproximació” el del mètode dels mínims quadrats.
Dit d’una altra manera, cal cercar els anomenats coeficients de regressió a 1 , a 2 , , a n , b , tals que facin mínima la distància al quadrat d 2 y, a 1 x 1 + + a n x n +b Si hom representa els valors de les variables estadístiques en l’espai ℝ n + 1 , aleshores l’hiperplà y = a 1 x 1 + + a n x n + b és dit de regressió per a n = 1, hom té la recta de regressió , i per a n = 2, el pla de regressió En el cas que n = 1, la recta de regressió y = ax + b té per coeficients on x i , y i són els valors de les variables, i x, y , les seves esperances o valors mitjans En el…
càlcul de variacions
Matemàtiques
Estudi de la teoria dels extrems d’integrals definides tals, que llur integrant és una funció coneguda d’una o més variables independents, d’una o més variables dependents i de les seves derivades.
El problema consisteix a determinar les variables dependents, de manera que la integral sigui màxima o mínima En el cas més simple, la integral és de la forma on cal determinar la funció y x de manera que I sigui màxima o mínima També poden ésser considerades integrals de la forma on y 1 , , y n són funcions de x desconegudes o bé integrals múltiples tals com on z = z x,y és desconeguda com també poden ser-ho com integrals múltiples d’ordre superior o de diverses variables dependents L’integrant pot ésser també una funció en la qual intervinguin derivades parcials d’ordre superior En el…
eficiència
Matemàtiques
Quocient entre la variància d’un estimador no esbiaixat i la mínima variància possible.
Pedro Nunes
Astronomia
Matemàtiques
Astrònom i matemàtic portuguès.
Conegut també amb el nom llatinitzat de Petrus Nonius , inventà el doble regle graduat, capaç d’apreciar fraccions de longitud inferiors al mig millímetre nònius Cosmògraf reial i professor a Coïmbra, escriví De arte atque ratione navigandi 1546, on indicà que la distància mínima entre dos punts de la superfície terrestre no és donada per la corba que talla els meridians amb un angle constant, sinó per l’arc de cercle màxim És autor, també, d’un tractat d’àlgebra i donà la solució correcta al problema del crepuscle més curt
tribu
Matemàtiques
Família de subconjunts d’un conjunt Ω.
Presenta tres propietats per a tot element de la família, el seu complementari també hi pertany per a tota successió A n n ∈ℕ d’elements de la família, ∪ A n també hi pertany i el conjunt Ω pertany a la família La tribu generada per una família de subconjunts M és la intersecció de totes les tribus que contenen M i resulta la mínima tribu que conté M Així, donat un conjunt Ω, el conjunt R Ω de les parts de Ω és una tribu a més, és la més gran de totes les tribus de conjunts de Ω La tribu de Borel o dels borelians de ℝ és la generada per tots els intervals oberts de ℝ
Pierre Louis Moreau de Maupertuis
Matemàtiques
Matemàtic bretó.
Estudià la carrera militar El 1735 dirigí l’expedició a Lapònia que pretenia de mesurar la longitud d’un arc de meridià d’1° de longitud angular, per tal de determinar després l’aplatament de la Terra comparant el resultat d’aquesta mesura amb l’obtingut en una altra latitud geogràfica L’any 1744 enuncià el principi de la mínima acció , conegut també com a principi de Maupertuis , a partir de la hipòtesi que Fermat establí en òptica referent al camí dels raigs lluminosos L’any 1746 fou nomenat president de l’acadèmia reial de Prússia, però més tard abandonà aquest càrrec i es…
mètode dels mínims quadrats
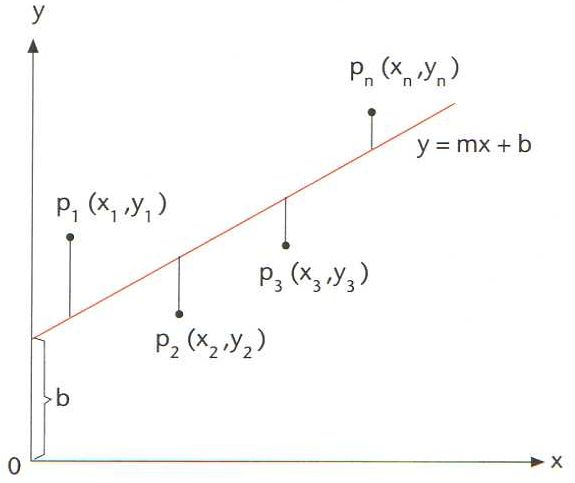
Representació de la recta y=mx + b obtinguda pel mètode dels mínims quadrats
© Fototeca.cat
Matemàtiques
Donat un conjunt de n punts del pla (x1, y1), (x2, y2), ... (xn, yn), mètode que permet de trobar l’equació y = mx + b de la recta que compleix la condició d’ésser la que més s’apropa als punts donats.
Hom defineix matemàticament la dita condició exigint que la suma dels quadrats de les desviacions, ha d’ésser mínima, entenent per desviació en un punt x i , y i la diferència d i = y i - mx i + b Hom pot demostrar que aquella condició condueix a les dues equacions a partir de les quals hom pot calcular els coeficients m i b de la recta, la qual és anomenada també recta de regressió D’altra banda, el mètode dels mínims quadrats serveix també per a ajustar funcions més complexes que la d’una recta, tals com funcions polinòmiques, exponencials, etc, i és utilitzat en l’estudi…
catenoide
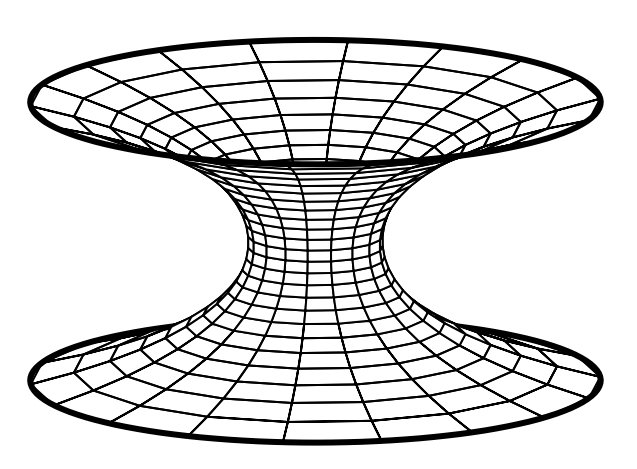
catenoide
Matemàtiques
Superfície mínima de revolució generada per una catenària que gira al voltant de l’eix d’abscisses.
Carl Friedrich Gauss
Carl Friedrich Gauss
Matemàtiques
Matemàtic alemany.
De família humil, extraordinàriament dotat per a les matemàtiques, pogué rebre ensenyament superior gràcies a la protecció del duc de Brunsvic, que l’envià a la Universitat de Göttingen Director de l’observatori i professor d’astronomia en aquella ciutat, hi residí fins a la mort, dedicat totalment a una fecunda tasca intellectual Els matemàtics li deuen aportacions transcendentals en la teoria dels nombres i en l’àlgebra noció de congruència i notació corresponent, sistematització de l’ús de demostració rigorosa del teorema fonamental de l’àlgebra, teoria de determinants , etc, qüestions…
problema de Fermat
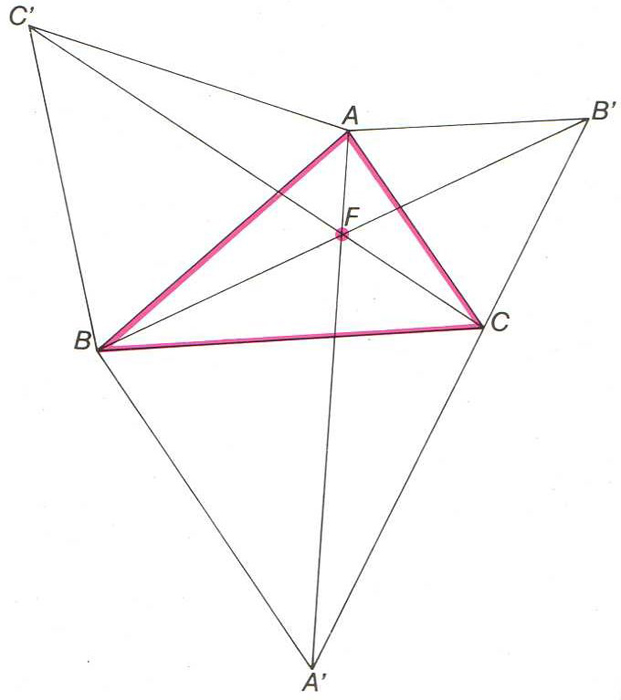
Problema de Fermat
© fototeca.cat
Matemàtiques
Donat un triangle ABC, problema que consisteix a trobar un punt M del pla per al qual la suma MA + MB + MC, és mínima.
El problema admet com a solució el punt de Fermat , si els tres angles del triangle són menors que 120°