Resultats de la cerca
Es mostren 11 resultats
políedres de Catalan
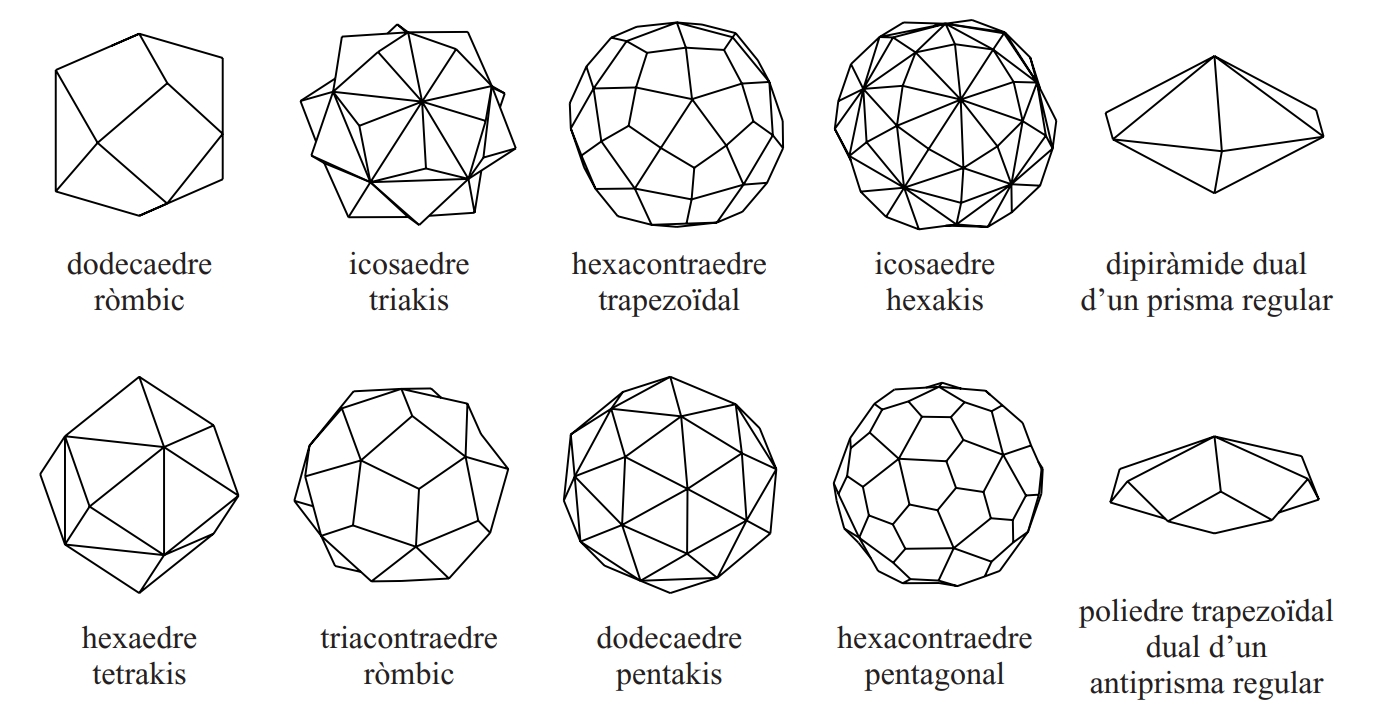
políedres de Catalan
políedre
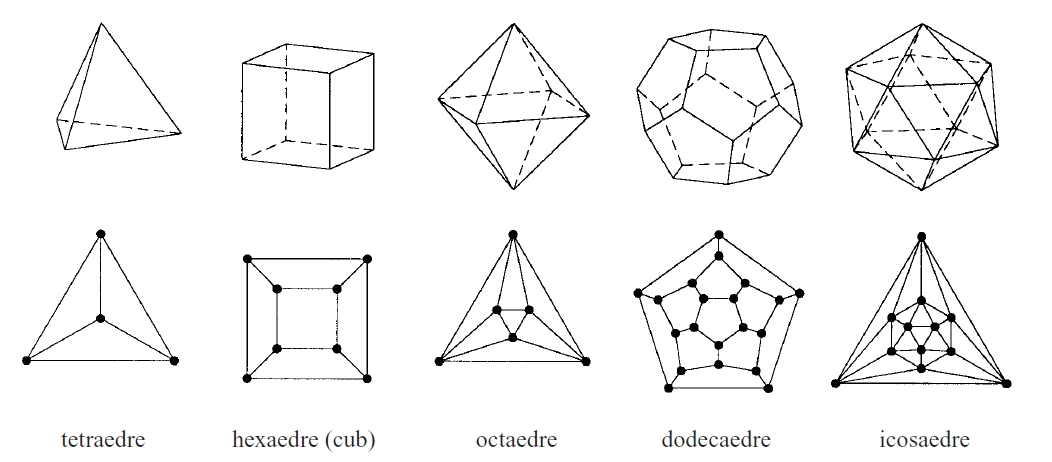
Els cinc políedres regulars i els diagrames de Schlegel associats
© Fototeca.cat
Matemàtiques
Sòlid limitat per quatre o més polígons anomenats cares.
Les interseccions de les cares constitueixen les arestes , i les interseccions de les arestes, els vèrtexs Un políedre és convex si qualsevol secció plana del políedre és un polígon convex Un políedre és còncau si no és convex Un políedre és simple si és topològicament equivalent a una esfera, és a dir, si no té forats Un políedre és regular si té les cares iguals i els angles iguals, essent les cares polígons regulars Des de la Grècia antiga hom sap que existeixen solament cinc políedres regulars el tetràedre regular , l’…
políedre estelat
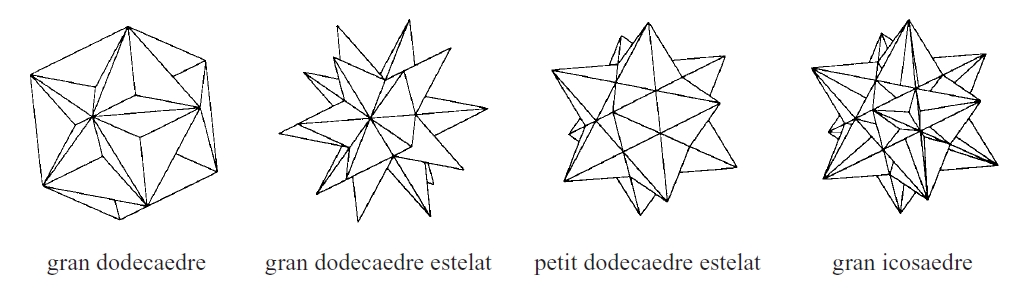
Els quatre políedres estelats regulars
Matemàtiques
Políedre que s’obté de col·locar piràmides sobre les cares d’un políedre convex o de prolongar-ne les cares.
aresta
Matemàtiques
Línia recta formada per la intersecció de dos plans, que determinen un angle dièdric.
En els políedres les arestes surten com a intersecció de dues cares i uneixen dos vèrtexs
polítop
Matemàtiques
Conjunt de punts de l’espai ℝn limitat per hiperplans.
La noció de politop generalitza la de polígon i la de políedre De fet, els politops de ℝ 2 són els polígons i els politops de ℝ 3 són els políedres Un exemple de politop a ℝ 4 és el tesseractis , que és l' hipercub de quatre dimensions
àrea
Matemàtiques
Mesura o grandor de l’extensió o porció del pla ocupada per una figura.
La teoria elemental de les àrees dels polígons pren com a unitat d’àrea el quadrat que té per costat la unitat de longitud Un rectangle de costats de longitud entera conté tants quadrats unitat com indica el producte de les seves dimensions Si les mesures dels costats del rectangle són fraccionàries hon divideix els costats en parts iguals, tantes com indiquen els denominadors d’aquelles mesures Resulta sempre la mateixa regla hom obté l’àrea d’un rectangle multiplicant les seves dues dimensions Si les mesures dels costats són irracionals hom pren aproximacions per defecte i per excés L’àrea…
piràmide
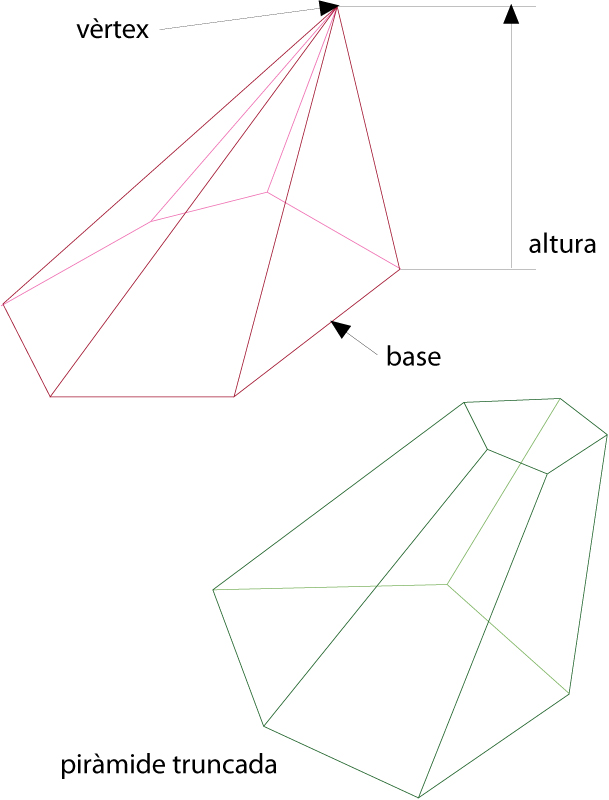
Piràmide irregular de base hexagonal i piràmide truncada de base pentagonal
© Fototeca.cat
Matemàtiques
Políedre que té per base un polígon qualsevol i les altres cares del qual (anomenades cares de la piràmide) són triangles que tenen un vèrtex comú (anomenat vèrtex de la piràmide).
Una piràmide és anomenada triangular tetràedre, quadrangular, pentagonal , etc, segons que la base sigui, respectivament, un triangle, un quadrilàter, un pentàgon, etc Una piràmide és anomenada regular si la base és un polígon regular i les cares són triangles isòsceles Hom anomena altura d’una piràmide la distància del vèrtex al pla del polígon El volum de la piràmide és el terç de la superfície de la base per l’altura Tallant una piràmide amb un pla hom obté dos políedres El políedre que conté el vèrtex és també una piràmide L’altre rep el nom de piràmide truncada
centroide
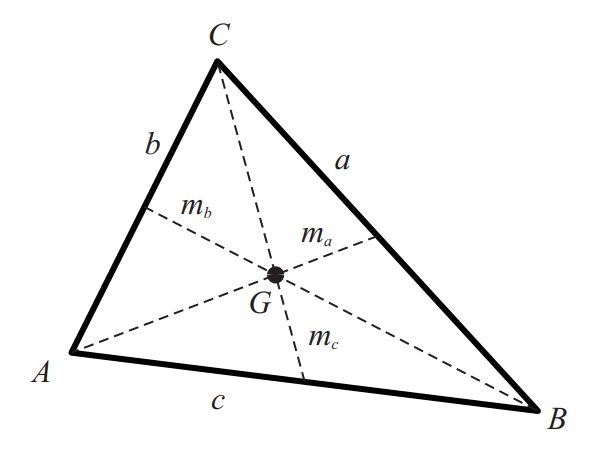
del triangle ABC
Física
Matemàtiques
Punt especial associat a una figura o a una distribució de punts que en el cas físic correspon al centre de massa o de gravetat, de vegades anomenat també baricentre.
En algunes figures el seu centroide és determinat geomètricament Per exemple, en un triangle és el punt d’intersecció de les mitjanes, i en els polígons políedres regulars és el centre de la circumferència esfera circumscrita Donat un conjunt discret de punts x 1 ,, x n amb masses m 1 ,, m n , punt que té per coordenades la mitjana de les coordenades dels punts ponderada per les masses En altres figures es poden trobar per integració les expressions de les coordenades del centroide Així, en figures amb una distribució de massa contínua φ x , el centroide és el punt x̄ = ƒφ x xdx…
piramidat | piramidada
Matemàtiques
Dit dels políedres les cares dels quals són piràmides regulars.
número d’or
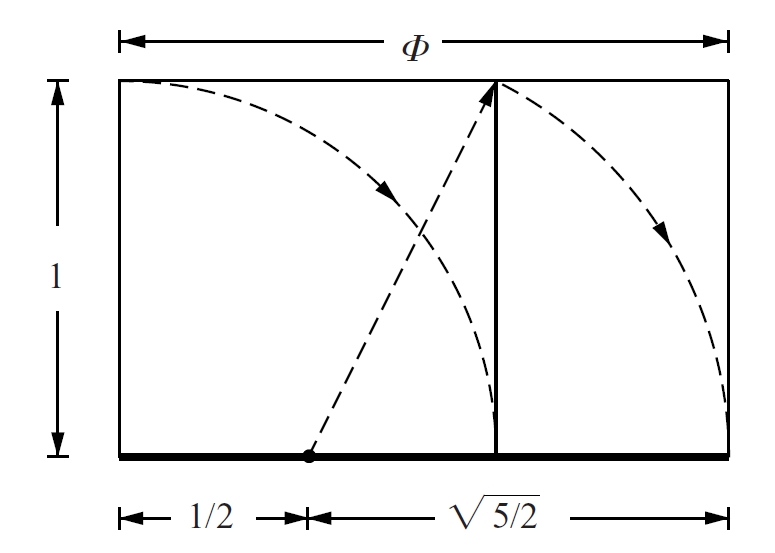
número d’or
Matemàtiques
Nombre irracional algebraic positiu que, elevat al quadrat, és igual a ell mateix més una unitat: (1 + ⎷5 ) ⁄ 2 = 1,618.
El número d’or apareix en molts problemes geomètrics relatius a les divisions harmòniques de segments o a proporcions de rectangles, o entre mides Així, un rectangle té de proporció el número d’or si, i solament si, té la mateixa proporció del rectangle que resulta de treure del rectangle original un quadrat Aquest nombre és el límit dels quocients 1 ⁄ 1, 2 ⁄ 1, 3 ⁄ 2, 5 ⁄ 3 dels termes de la successió de Fibonacci i té una important presència en elements naturals i artístics, especialment en pintura i arquitectura, ja que que el número d’or és igual al cosinus de 36º i, per tant, està lligat…