Resultats de la cerca
Es mostren 8 resultats
borelià
Matemàtiques
Element d’una tribu de Borel o, a vegades, la tribu pròpiament.
funció periòdica
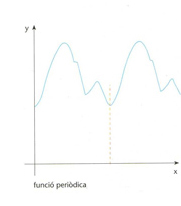
Funció periòdica
© Fototeca.cat
Matemàtiques
Funció f
: D
⊂ℝ→ℝtal que existeix un nombre T
∈ℝ-{0} que satisfà que, per a tot x
∈ D, x
+ T∈ D
i f
( x
+ T
)= f
( x
).
Hom diu aleshores que T és un període de la funció f bé que hom anomena, pròpiament, període al més petit nombre T que satisfà les condicions esmentades En són exemples les funcions trigonomètriques sinus i cosinus que tenen un període 2π
mesura
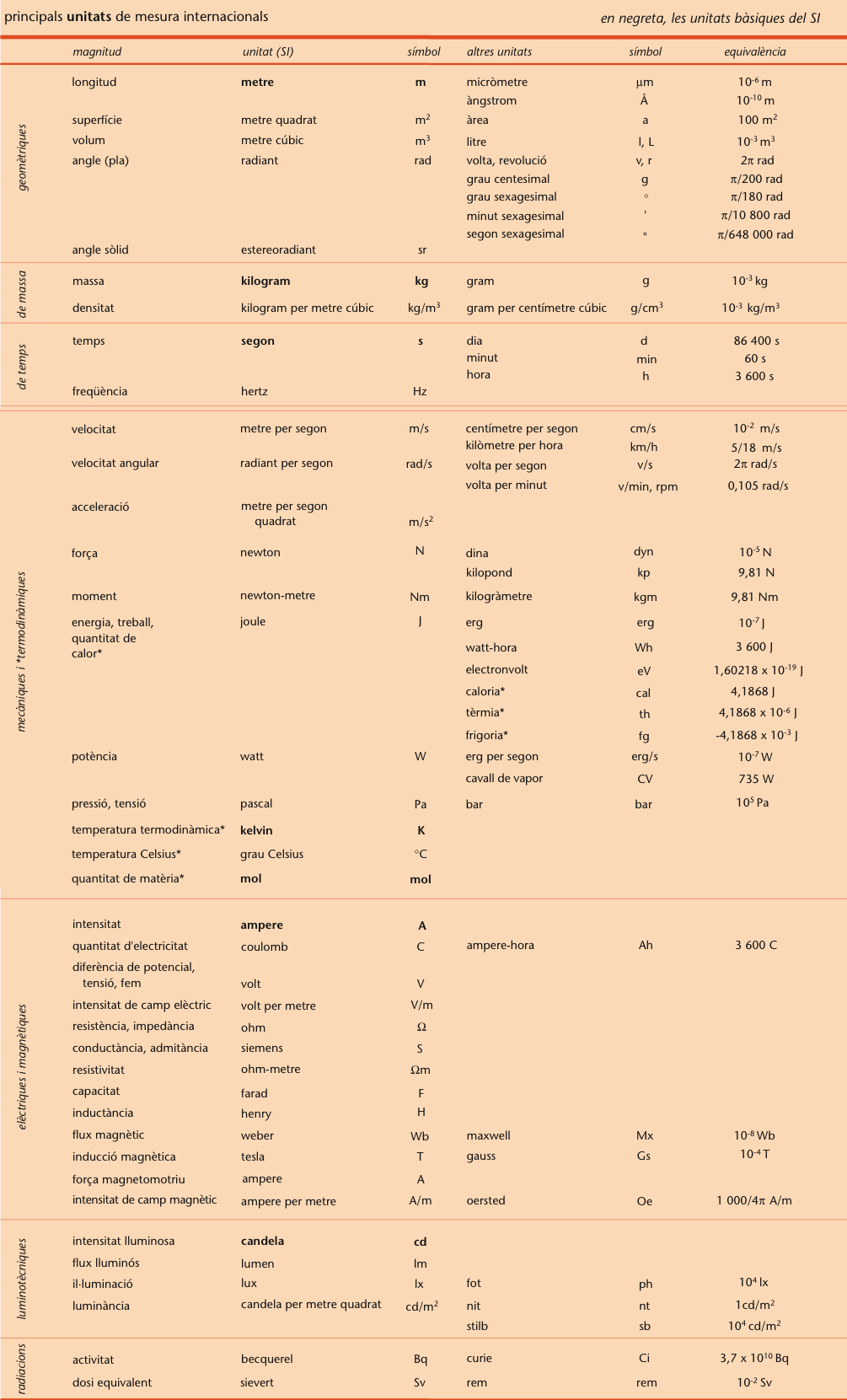
Principals unitats de mesura internacional
© Fototeca.cat
Física
Matemàtiques
Valor numèric obtingut experimentalment com a resultat d’un mesurament consistent a comparar una magnitud amb una altra de la mateixa espècie elegida com a unitat
, amb la finalitat d’establir unes relacions o la deducció d’unes conclusions.
Certes mesures, però, poden ésser de tipus qualitatiu “sí o no”, “més gran que o igual a”, “lineal”, etc, o poden estar relacionades amb una entitat gràfica d’imatge que serà donada per una “concentració” o per una probabilitat obtinguda per repetició del fet experimental El procés de mesura ha d’ésser objectiu i, per tant, la comparació ha d’ésser feta amb una magnitud unitat de la mateixa espècie i de similar dimensió Si hom l’efectua per un procés indirecte transductor, la magnitud final ha d’ésser calibrada en unitats de la magnitud primitiva No totes les magnituds són mesurables en un…
metamatemàtica
Matemàtiques
Nom donat per Hilbert a l’estudi del llenguatge format pels enunciats sobre els signes emprats per la matemàtica.
Així, l’enunciat ''tot x més gran que 2 , si és primer és senar’ és un enunciat pròpiament matemàtic, és a dir, un teorema del qual hom pot provar la correcció o la incorrecció a partir d’un determinat conjunt d’axiomes en canvi, són metamatemàtics els enunciats '' x és una variable numèrica’, '' 2 és una constant numèrica’, etc, que caldria que acompanyessin l’enunciat matemàtic anterior per tal de fer-lo comprensible a qui no sabés què representen x i 2 La distinció entre matemàtica i metamatemàtica fou feta per Hilbert a fi d’aconseguir el desenvolupament d’una teoria de la…
paradoxa
Lògica
Matemàtiques
Enunciat o raonament que porta a dues conclusions mútuament contradictòries però de cap de les quals hom no pot prescindir.
Sovint identificable amb l'antinòmia i àdhuc amb l'aporia, la paradoxa, que té un significat més ampli que l’una i l’altra, sol ésser tipificada en l’afirmació del mentider, quan diu “ara dic mentida” si és veritat que diu mentida, és que menteix, però està dient la veritat, o sia que no està mentint i, si no és veritat que diu mentida, menteix, però no és veritat que digui mentida Les paradoxes d’aquesta mena, consistents en una autoreferència i que solen ésser típiques en les anomenades paradoxes semàntiques o lingüístiques, han estat estudiades des de sempre i hom només ha pogut trobar-ne…
nombre
Matemàtiques
Resultat de comptar les coses que formen un agregat (dos, tres, quatre, etc., i també un, o sia, la unitat) o qualsevol dels ens abstractes que resulten de generalitzar aquest concepte.
El concepte de nombre ha anat evolucionant al llarg de la història així, al principi anava enllaçat amb el simple ús de xifres o guarismes per a comptar sistemes de numeració Els nombres 1, 2, 3, 4, etc, ja eren usats en les antigues cultures babilònica, egípcia, xinesa la qual coneixia els negatius i índia la qual introduí el zero Aquest ús de xifres no implicava, però, cap concepte abstracte de nombre A l’antiga Grècia els pitagòrics consideraren que el nombre era una estructura determinada, immanent a totes les coses això generà la numerologia grega o mística, basada en les propietats…
topologia

Topologia Les figures unides amb fletxes són topològicament iguals, perquè és possilbe passar de l’una a l’altra per mitjà d’una transformació contínua
© Fototeca.cat
Matemàtiques
Part de la matemàtica que estudia aquelles propietats dels conjunts de punts de la recta, del pla, de l’espai o d’espais de dimensions superiors que no són alterades per les transformacions contínues.
Es tracta de propietats geomètriques que no depenen de cap magnitud, sinó únicament de la posició relativa dels punts Per exemple, el fet que dos punts puguin unir-se o no per un camí, o que el nombre de cares menys el d’arestes més el de vèrtexs d’un políedre esfèric sigui sempre dos teorema d’Euler Aquí hom entén per transformació contínua aquella que admet una inversa i que tant ella com la inversa són contínues L’íntima connexió que hi ha entre el concepte de continuïtat d’una funció en un punt i el d’entorn d’un punt permet de transportar l’estudi de propietats topològiques a aquells…
conjunt

Representació gràfica de la relació de pertinença i de les operacions d’unió i intersecció dels conjunts
© Fototeca.cat
Matemàtiques
Reunió d’objectes ben definits en la intuïció o en el pensament, considerada com una totalitat (Cantor).
Aquesta definició, des del punt de vista matemàtic, no és vàlida, i, així, en matemàtiques la noció de conjunt no és definida, i s’inclou dins del desenvolupament d’una teoria axiomàtica que eviti les paradoxes i contradiccions com les que, a començament del segle XX, posaren en qüestió no solament la teoria de conjunts, sinó bona part de la matemàtica Hom no defineix, doncs, ni conjunt, ni element, ni la relació de pertinença, i es conforma amb la idea intuïtiva del que signifiquen frases com Un conjunt és format per elements, o l’element 4 pertany al conjunt dels nombres naturals La…