Resultats de la cerca
Es mostren 202 resultats
núvol de punts
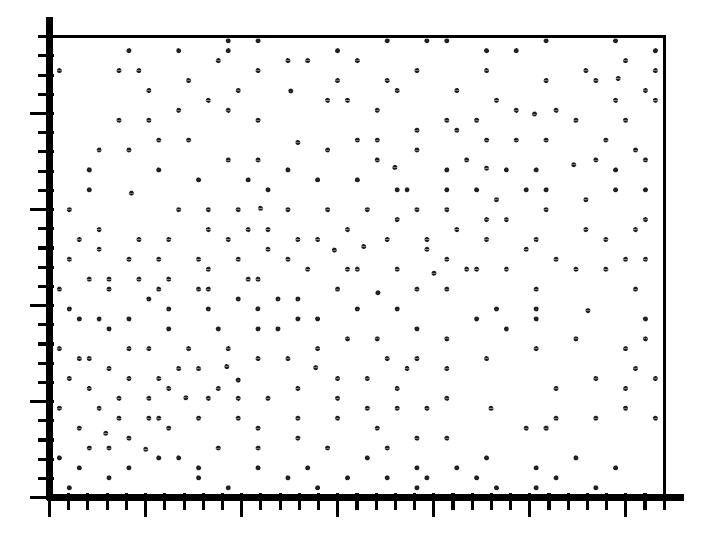
núvol de punts
Matemàtiques
Conjunt de punts del pla o de l’espai que visualitzen els valors de diverses variables estadístiques la dependència de les quals es vol estudiar.
punts de Brocard
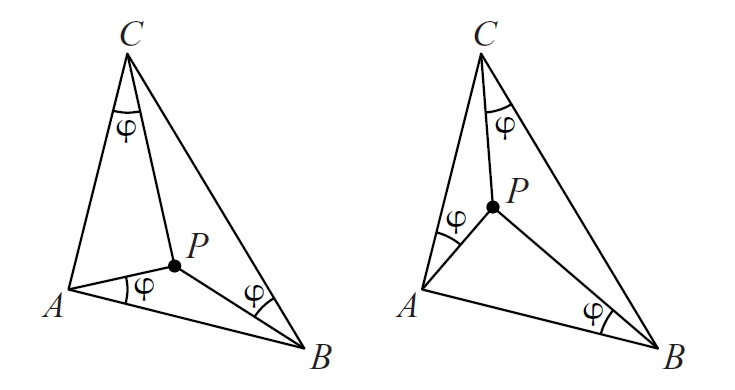
punts de Brocard
© fototeca.cat
Matemàtiques
Punts P d’un triangle ABC tals que els angles PBC, PCA i PAB són iguals.
En tot triangle n’hi ha dos
teorema de la circumferència dels nou punts
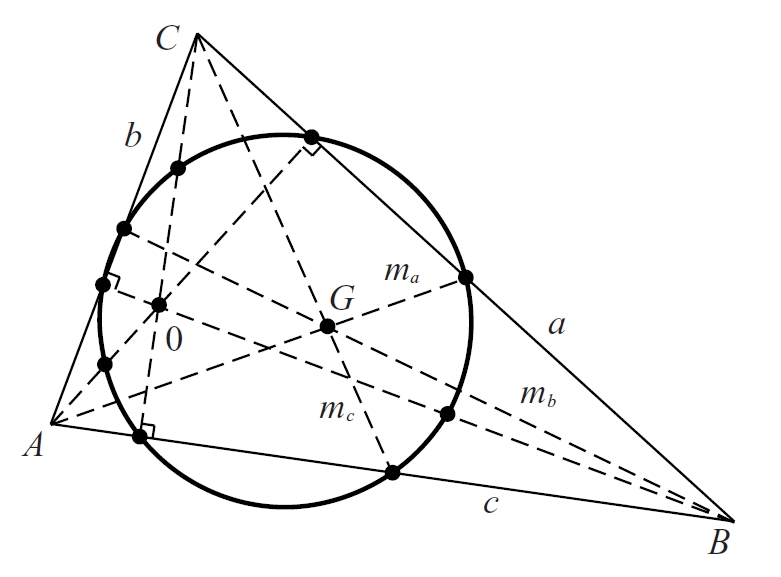
Teorema de la circumferència dels nou punts
Matemàtiques
Propietat segons la qual els peus de les altures, els peus de les mitjanes i els tres punts mitjans dels segments que van de l’ortocentre als vèrtexs del triangle són en una circumferència, anomenada circumferència dels nou punts.
perspectiva cònica
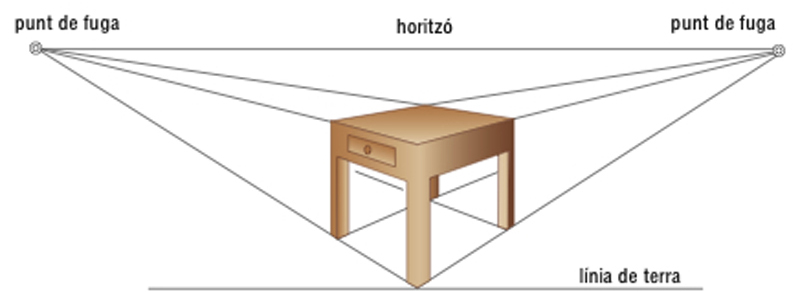
Representació d’una taula en perspectiva cònica obliqua (dos punts de fuga)
© Fototeca.cat
Art
Disseny i arts gràfiques
Matemàtiques
Perspectiva central el centre de projecció o pol de la qual és l’ull de l’observador.
Per al traçat d’aquesta perspectiva, hom admet que la llum que arriba a l’ull procedent de qualsevol punt d’un objecte és una línia recta, que rep el nom de raig visual Els principals elements per al seu traçat són la posició de l’ull o punt de vista , de la qual depèn l’efecte de la perspectiva l' horitzó o la línia horitzontal traçada en el pla del quadre, a l’alçada del punt de vista, que ocupa en el quadre la mateixa posició que la perspectiva de l’horitzó natural el pla geometral , que és el pla perpendicular al pla del quadre i on hom suposa que són situats l’observador i els objectes…
geodèsica
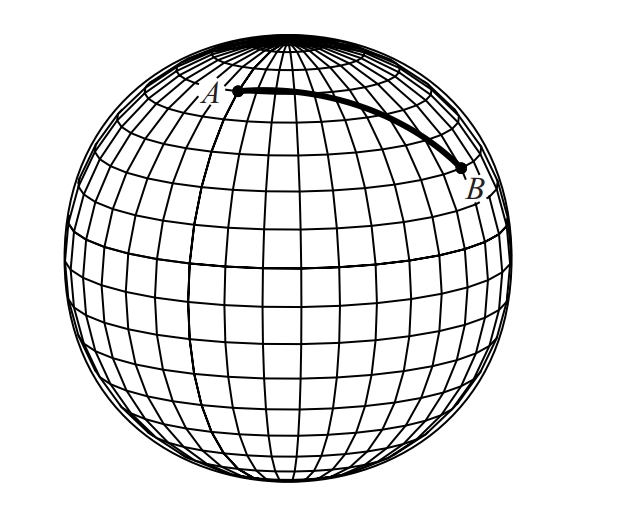
Geodèsica de l’esfera entre els punts A i B
© Fototeca.cat
Geologia
Matemàtiques
Entre dos punts d’una superfície, corba de longitud mínima que està continguda en la superfície; en el pla, les geodèsiques són segments rectilinis; en una esfera, són arcs de cercle màxim; en un cilindre, són hèlixs.
axiomes de separació
Matemàtiques
Axiomes topològics relatius a les possibles separacions entre punts.
En un espai topològic Y , els axiomes són Axioma T 0 Per a qualsevol parell de punts x i y diferents, existeix un entorn de x que no conté y Axioma T 1 Per a qualsevol parell de punts x i y diferents, existeixen un entorn U de x , i un entorn V de y , tals que U no conté y i V no conté el punt x Quan aquest axioma se satisfà, l’espai es diu espai de Fréchet Axioma T 2 Per a qualsevol parell de punts x i y diferents, existeix un entorn de x i un entorn de y sense punts en comú Quan aquest axioma se satisfà, l’espai s’anomena espai de…
projectivitat
Matemàtiques
Transformació projectiva, és a dir, aplicació injectiva entre dos plans projectius no necessàriament diferents (f: p* →p*’, que transforma conjunts de punts col·lineals en conjunts de punts col·lineals.
L’estudi de les propietats del pla projectiu invariants sota una projectivitat són l’objecte d’estudi de la geometria projectiva Si f és una projectivitat, es demostra que el transformat x' , y' d’un punt x , y es troba per les equacions i que tota transformació donada per les anteriors equacions és una projectivitat plana, és a dir, que els punts x, y tals que a 3 x + b 3 y + c 3 = 0 es transformen en els punts impropis del pla projectiu
lemniscata
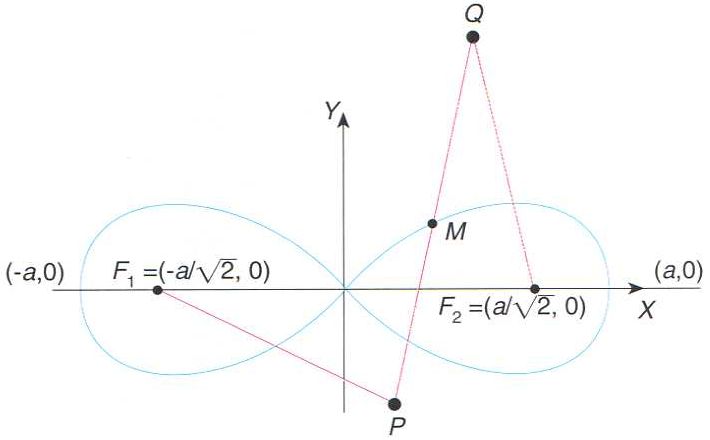
Contrucció geomètrica de lemniscata: ès el lloc geomètric dels punts M situats al mig d’un segment de longuitud constant, que uneixen dos punts, P i Q, que descriuen circumferències de radis a i de centres en el focus F1 i F2
© Fototeca.cat
Matemàtiques
Corba algèbrica de quart grau que té una forma semblant a la d’un vuit.
És coneguda també com a lemniscata de Bernoulli , i pot ésser expressada per l’equació x 2 + y 2 2 = a 2 x 2 - y 2
arc de Jordan
Matemàtiques
Arc el conjunt de punts del qual és homeomorf amb un interval real.
Intuïtivament és el resultat d’estirar i tòrcer un fil elàstic, sense trencar-lo i sense que coincideixin dos dels seus punts
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina