Resultats de la cerca
Es mostren 17 resultats
quàrtic | quàrtica
resolvent
Matemàtiques
Donada una equació de quart grau amb solucions x1, x2, x3, x4 , equació de tercer grau que té com a solucions (x1+x2 ) · (x3+x4 ), (x1+x3 )·(x2+x4 ) i (x1+x4 )·(x2+x3 ).
Si l’equació de quart grau és de la forma x 4 +px 2 +qx+r = 0 la seva resolvent és y 3 -2py 2 + p 2 -4r y + q 2 = 0 A partir de les solucions d’aquesta equació cúbica hom n'obté fàcilment les de l’equació original
lemniscata
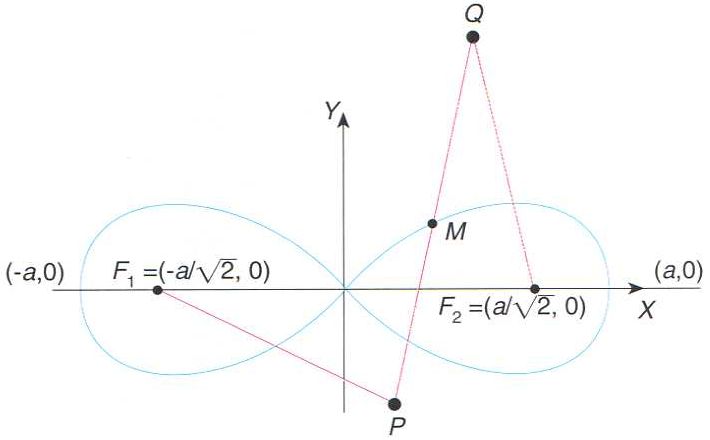
Contrucció geomètrica de lemniscata: ès el lloc geomètric dels punts M situats al mig d’un segment de longuitud constant, que uneixen dos punts, P i Q, que descriuen circumferències de radis a i de centres en el focus F1 i F2
© Fototeca.cat
Matemàtiques
Corba algèbrica de quart grau que té una forma semblant a la d’un vuit.
És coneguda també com a lemniscata de Bernoulli , i pot ésser expressada per l’equació x 2 + y 2 2 = a 2 x 2 - y 2
quadrant
Matemàtiques
Cadascuna de les quatre parts en què un pla és dividit per dos eixos de coordenades rectangulars.
Són anomenats primer, segon, tercer i quart quadrant , prenent com a primer el superior de la dreta i comptant-los en el sentit antihorari
Ernst Eduard Kummer
Matemàtiques
Matemàtic alemany.
Es destacà sobretot per la introducció dels nombres ideals i pel descobriment de la superfície algèbrica de quart ordre que porta el seu nom
Ludwig Otto Hesse
Matemàtiques
Matemàtic alemany.
S'especialitzà en l’estudi de les corbes de tercer i quart ordre i introduí el determinant invariant que és conegut amb el nom de hessià
Ludovico Ferrari
Matemàtiques
Matemàtic italià.
Estudià i es doctorà a Bolonya Deixeble de Cardano, fou professor a les universitats de Milà 1543 i de Bolonya 1565 Determinà 1545 un mètode per a resoldre l’equació general de quart grau, gràcies a una equació auxiliar de tercer grau
Ars magna
Matemàtiques
Tractat d’àlgebra de Gerolamo Cardano editat a Nuremberg el 1545.
Representa el primer intent de teoria sistemàtica d’equacions, i inclou alguns càlculs amb nombres negatius, bé que ell mateix no els admetia També conté els treballs posteriors del seu deixeble Ludovico Ferrari, amb l’estudi de les equacions de quart grau i llurs solucions L’aparició d’aquesta obra inicià la controvèrsia entre Tartaglia i Cardano
Jakob Steiner
Matemàtiques
Matemàtic suís.
Analfabet fins a 14 anys, estudià amb Pestalozzi, i després a Heidelberg i Berlín, on fou nomenat professor extraordinari el 1934 Féu recerques importants en geometria superfícies cúbiques i de quart ordre i geometria projectiva, amb els seus mètodes sintètics Publicà Systematische Entwicklung der Abhängigkeit geometrischer Gestalten von Einander ‘Desenvolupament sistemàtic de la interdependència de les figures geomètriques’, 1932 i pòstumament 1882 aparegueren les seves obres completes Ideà, entre altres, el teorema que du el seu nom
Joseph-Louis Lagrange
Matemàtiques
Matemàtic francès.
Continuador de l’obra d’Euler, fou cridat a Prússia per Frederic el Gran Traslladat definitivament a París el 1787, posà de manifest a l’École Polytechnique els seus amplis coneixements estudiant les equacions de grau superior al quart, indicà les bases de la futura teoria de grups Ideà el mètode d' interpolació que duu el seu nom És autor de Mécanique analytique 1788, Traité de la résolution des équations numériques 1798 i Leçons sur le calcul des fonctions 1799 La seva obra completa fou publicada a París del 1867 al 1892