Resultats de la cerca
Es mostren 5 resultats
rotació
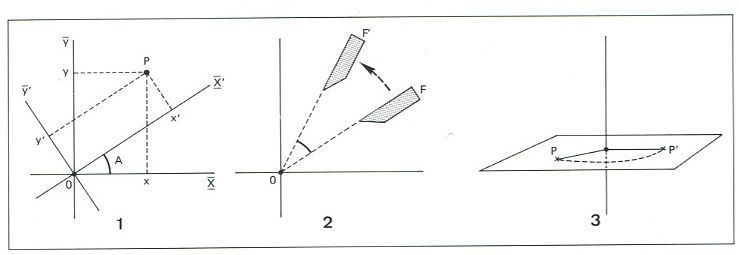
rotació: 1, d'eixos; 2, al voltant d'un punt0; 3, al voltant d'un eix
Matemàtiques
Transformació geomètrica que constitueix un dels moviments rígids del pla o de l’espai i que conserva les distàncies (mides i forma) i l’orientació de les figures sobre les quals és aplicada.
En el pla hom considera la rotació al voltant d’un punt fix que correspon a moviments rígids circulars de centre al punt donat En l’espai hom considera la rotació al voltant d’una línia , en la qual qualsevol punt d’una figura es mou en sentit circular al voltant de la línia donada eix de rotació, en un pla perpendicular a aquesta i que passa pel punt donat Una rotació d’eixos correspon a una rotació que deixa fix l’origen de coordenades Aquestes rotacions permeten de passar d’un sistema de referència a un altre que pot ésser…
semblança
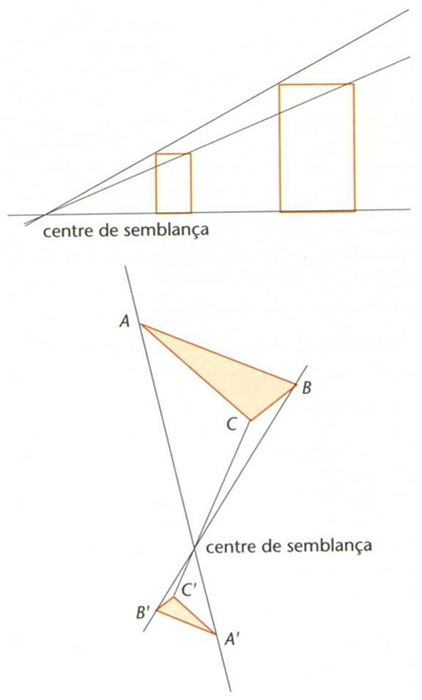
Dues semblances directes
© Fototeca.cat
Matemàtiques
Transformació geomètrica T de ℝn en ℝn tal que la distància entre les imatges de dos punts qualssevol és igual a la distància entre aquests dos punts multiplicada per una quantitat constant positiva dita raó de la semblança.
És a dir, d T x, T y = k, d x, y Dues figures són anomenades semblants si hi ha una semblança que transforma l’una en l’altra Les semblances conserven la forma de les figures però en canvien la grandària, eixamplant-la o reduint-la segons que la raó sigui respectivament major o menor que 1 Les semblances de raó 1 són dites isometries o moviments rígids , els quals són sempre el resultat de compondre una translació amb una transformació lineal ortogonal que conserva els angles Les homotècies són exemples típics de semblances Tota semblança és el resultat d’aplicar successivament…
Daniel Bernoulli
Biologia
Física
Matemàtiques
Físic, matemàtic i fisiòleg neerlandès.
Fill i nebot de matemàtics, s’inicià en la disciplina en la qual sobresortiren els seus antecessors, però aviat es decantà vers les ciències experimentals Després de fer estudis de medicina a Basilea, Heidelberg i Estrasburg es doctorà en aquests camp a vint-i-un anys, el 1724 publicà les Exercitationes quaedam mathematicae , que reflectien el seu interès per la matemàtica i en les quals tractava temes de probabilitat i la resolució de l’equació diferencial de Riccati Fou cridat a l’Acadèmia de Sant Petersburg on romangué del 1725 al 1733 Fou aquest el període més fèrtil de la…
,
subespai
Matemàtiques
Qualsevol subconjunt no buit F d’un espai vectorial E (sobre un cos K) tal, que és estable per a les dues lleis de E i que, proveït d’aquestes lleis induïdes, és també un espai vectorial (sobre K).
En l’espai vectorial de tres dimensions ℝ 3 els subespais són el mateix espai, l’origen de coordenades i totes les rectes i els plans que passen per l’origen F és un subespai de E si, donats qualssevol x , y de F i λ de K , aleshores la combinació lineal x ,-λ y pertany a F Tota família de vectors determina l’anomenada envolupant lineal , o mínim subespai, que els conté La intersecció M ∩ N de dos subespais M i N és un subespai, però la reunió M ∪ N no ho és en general La suma M + N definida per a tots els vectors que són suma d’un element de M i un de N és el mínim subespai que…
sanefa
Els set tipus de sanefes
Matemàtiques
Figura plana en la qual tots els moviments rígids que pertanyen al seu grup de simetria deixen una recta invariant i totes les translacions que hi pertanyen són múltiples d’una translació donada no nul·la, que marca el ritme de repetició de la figura. Hi ha set formes de generar sanefes en el pla.