Resultats de la cerca
Es mostren 59 resultats
radi
Matemàtiques
Distància del centre d’un cercle o d’una esfera a qualsevol punt de la circumferència del cercle o de la superfície esfèrica, respectivament.
radi vector
Matemàtiques
Vector que va des d’un origen o punt fix determinat (centre, pol, focus, etc) a un punt variable.
El radi vector d’una ellipse o d’una hipèrbola és definit com el que va des de qualsevol dels focus de la cònica fins a un punt variable d’aquesta
radi de curvatura
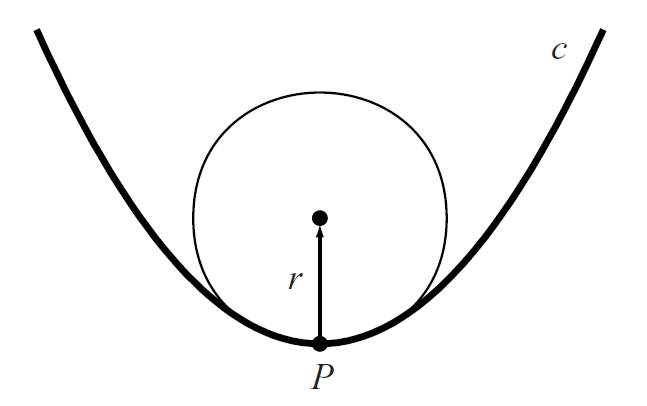
Radi de curvatura de la corba c en P
Matemàtiques
Invers de la curvatura d’una corba en un punt.
El radi de curvatura és el radi del cercle osculador
radi de curvatura
Matemàtiques
Radi d’una circumferència la curvatura de la qual coincideix amb la d’una corba en un punt donat.
Aquesta circumferència rep el nom de cercle de curvatura o bé cercle osculador El valor R del radi de curvatura és l’invers de la curvatura C El centre del cercle osculador rep el nom de centre de curvatura de la corba
esfera
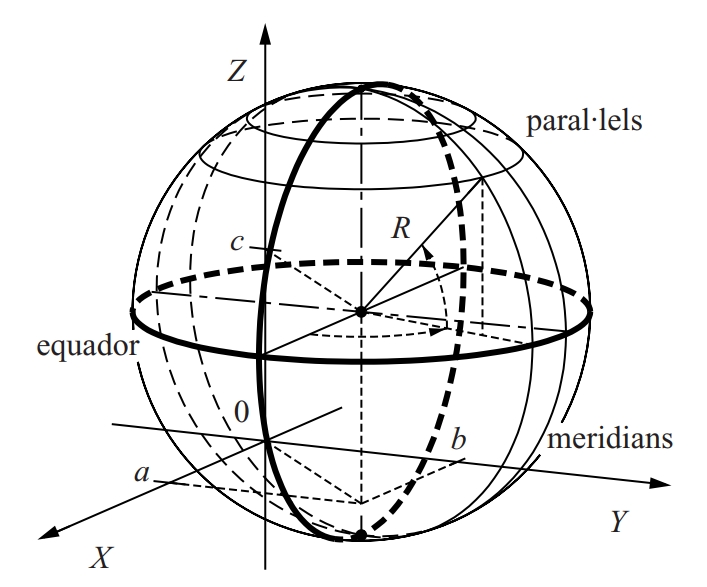
Esfera de centre (a, b, c) i radi R
Matemàtiques
Figura espacial generada per la rotació d’un cercle al voltant d’un dels seus diàmetres.
Es tracta d’una quàdrica amb equació cartesiana x – a 2 + y – b 2 + z – c 2 = R 2 si el centre és el punt a , b , c i el radi és R El seu volum val i la seva superfície S = 4 π R 2
cardioide
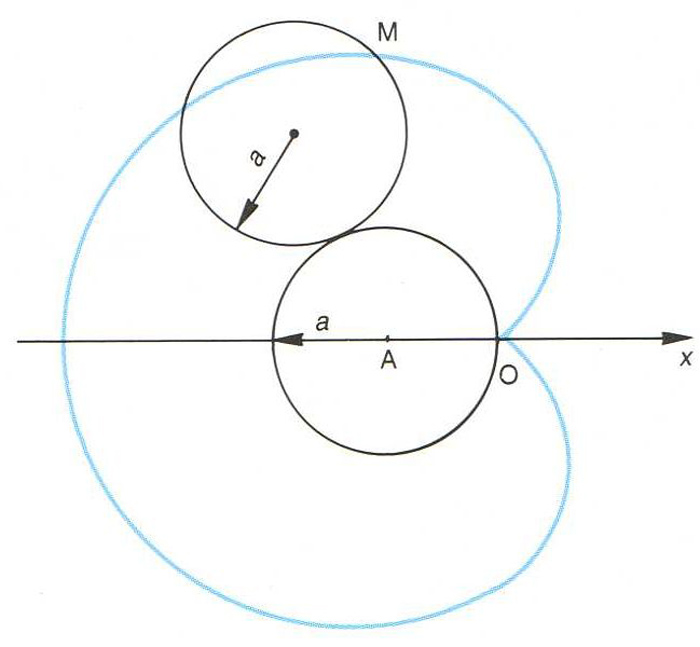
Cardioide determinada pel punt fix M d’un cercle de radi a que roda sense lliscar sobre un cercle fix de radi a i centre A. O és el punt de retrocés
© fototeca.cat
Matemàtiques
Epicicloide singular engendrada per les posicions d’un punt d’un cercle de radi a que roda sense lliscar per damunt d’un altre cercle del mateix radi.
Té un punt de retrocés O , respecte al qual l’equació de la cardioide en coordenades polars és ρ = 2 a 1-cos θ La longitud de la cardioide és aleshores 16 a i l’àrea és 6π a 2
circumferència
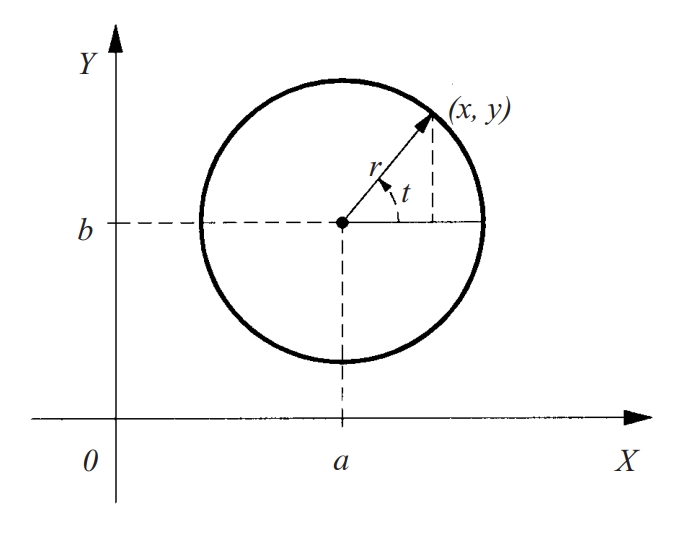
circumferència
Matemàtiques
Corba plana determinada pel conjunt de punts del pla la distància dels quals a un punt fix d’aquest pla (centre) és una constant (radi).
Si a , b és el centre i r el radi, la seva equació cartesiana és x – a 2 + y – b 2 = r 2 i les seves equacions paramètriques són x = a + r cos t , y = b + r sin t El perímetre val 2π r
superfície esfèrica
Matemàtiques
Superfície constituïda per tots els punts de l’espai que són a una distància (radi) fixa d’un punt fix (centre).
L’estudi de les figures que es poden traçar damunt una superfície esfèrica dóna lloc a la geometria esfèrica En són els elements fonamentals els punts i les circumferències màximes situades en plans que passen pel centre Figures importants són els triangles esfèrics , amb els quals hom pot fer càlculs per mitjà de la trigonometria esfèrica, que guarden un cert parallelisme amb els de la trigonometria plana La geometria esfèrica ha tingut un gran desenvolupament pel fet que la cosmografia estudia la posició dels astres com si fossin punts situats sobre una esfera de radi infinit i…
nefroide
Matemàtiques
Epicicloide amb r = 2a
.
És generada per un cercle de radi a que rodola sense lliscar per l’exterior d’un cercle de radi 2 a Té una longitud de 24 a i una àrea de 12 π a 2
esfera
Matemàtiques
En un espai mètric de distància d, conjunt de punts x la distància dels quals a un cert punt fix p és igual a un nombre real positiu r.
El centre de l’esfera és p i el radi r , i es denota per S p r A ℝ n l’esfera de centre 0 i radi 1 es denota per S n –1 i rep el nom d’ esfera unitat
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- Pàgina següent
- Última pàgina