Resultats de la cerca
Es mostren 8 resultats
fase
Física
Matemàtiques
Argument de les funcions sinusoïdals (sinus o cosinus), dependents del temps, especialment quan hom les considera en les formes u = U sin (ϖt+ϕ) i u = U cos (ϖt+ϕ).
És emprat per a descriure l’elongació d’un moviment harmònic o el valor d’una magnitud variable en corrent altern Dues magnituds u 1 i u 2 , variables periòdicament amb el mateix període, són en fase quan en tot instant tenen ambdues la mateixa fase altrament presenten una diferència de fase o desfasament , i hom diu que són desfasades Quan són desfasades π radiants hom diu que són en oposició , i quan ho són π/2 radiants, en quadratura El valor de la fase a l’instant t = 0 és anomenat fase inicial
valor principal
Matemàtiques
Per a una funció inversa trigonomètrica com arcsinus, arccosinus o arctangent, valor numèric més petit pres en un interval concret.
Així, el valor principal d’arcsin 1/2 és π/6, és a dir, que trobar el valor principal és reduir tots els valors possibles d’acord amb el mòdul 2π radiants
trocoide
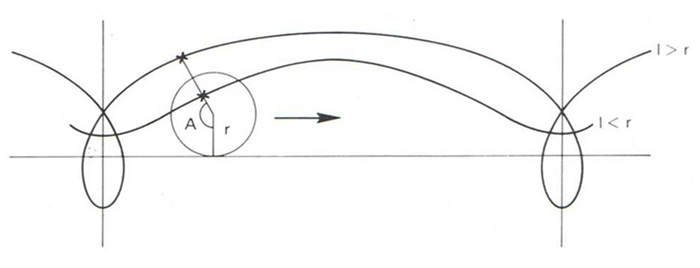
Trociode
© fototeca.cat
Matemàtiques
Corba descrita per un punt fixat a un cercle quan aquest cercle roda sense lliscament sobre una línia recta fixa.
Si el radi del cercle és r , la distància del punt generador al centre del cercle és l i A és l’angle determinat pel punt quan el cercle ha rodat A radiants, aleshores les equacions paramètriques de la trocoide són x = rA-l sin A y = r-l cos A Si l és major que r punt exterior al cercle, la trocoide descriu rulls si l és menor que r punt interior al cercle, la trocoide no toca mai la línia recta fixa base del desplaçament si el punt és el centre del cercle, la trocoide és una recta si l és igual a r punt de la circumferència, la trocoide és aleshores una cicloide
excés esfèric
Matemàtiques
En un triangle esfèric, d’angles A, B i C mesurats en radiants, quantitat donada per la fórmula E = A+B+C-π.
funció sinus
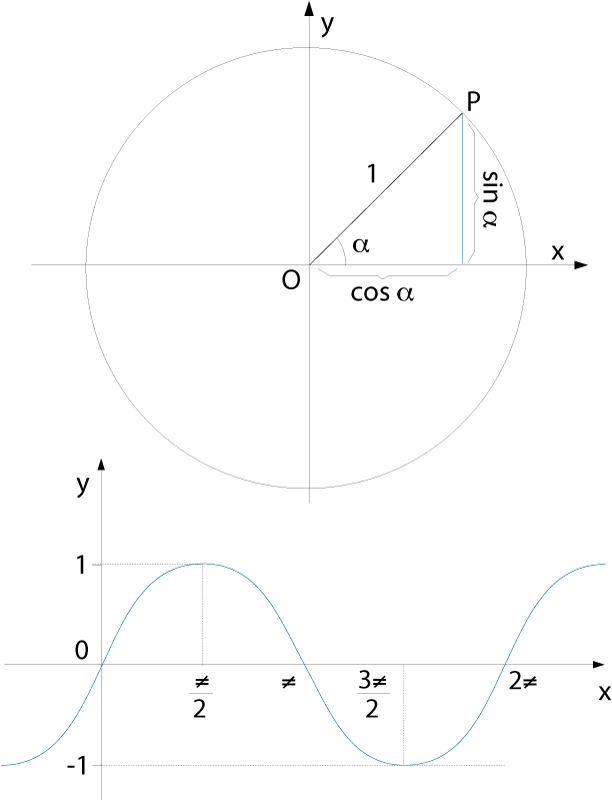
Representació gràfica del sinus d’un angle (a dalt) i de la funció sinus (a baix)
© Fototeca.cat
Matemàtiques
Funció sin: ℝ→ℝdefinida per l’assignació x →sin (x) on sin(x) és el sinus de l’angle que fa x radiants.
És una funció periòdica de període 2π i el seu recorregut és l’interval -1,1 És una de les sis funcions trigonomètriques o circulars i està relacionada amb la funció cosinus per la derivada d sin x / dx =cos x , d cos x / dx = -sin x És indefinidament derivable i el seu desenvolupament en sèrie entera és En termes de la funció exponencial complexa té l’expressió sin x= e i x - e i x /2 i , relació que permet d’estendre-la al cos dels nombres complexos, resultant-ne la funció sinus complex
funció cosinus
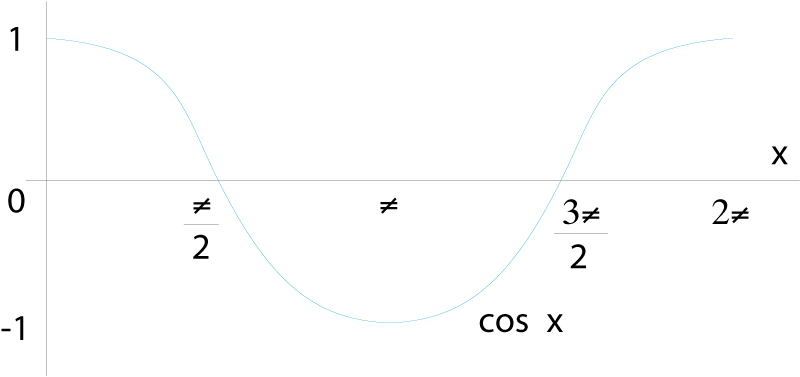
Representació gràfica de la funció y=cos x
© Fototeca.cat
Matemàtiques
Funció cos: ℝ→ℝdefinida per l’assignació x →cos (x), on cos(x) és el cosinus de l’angle que fa x radiants.
És una funció periòdica de període 2π i el seu recorregut és l’interval -1, 1 És una de les sis funcions trigonomètriques o circulars i està relacionada amb la funció sinus per la derivada dcos x/ dx = -sin x, dsin x/ dx = cos x És indefinidament derivable, i el seu desenvolupament en sèrie entera és En termes de la funció exponencial complexa té l’expressió cos x=e i x + e - i x /2, relació que permet d’estendre-la al cos dels nombres complexos, resultant-ne la funció cosinus complex
funció tangent
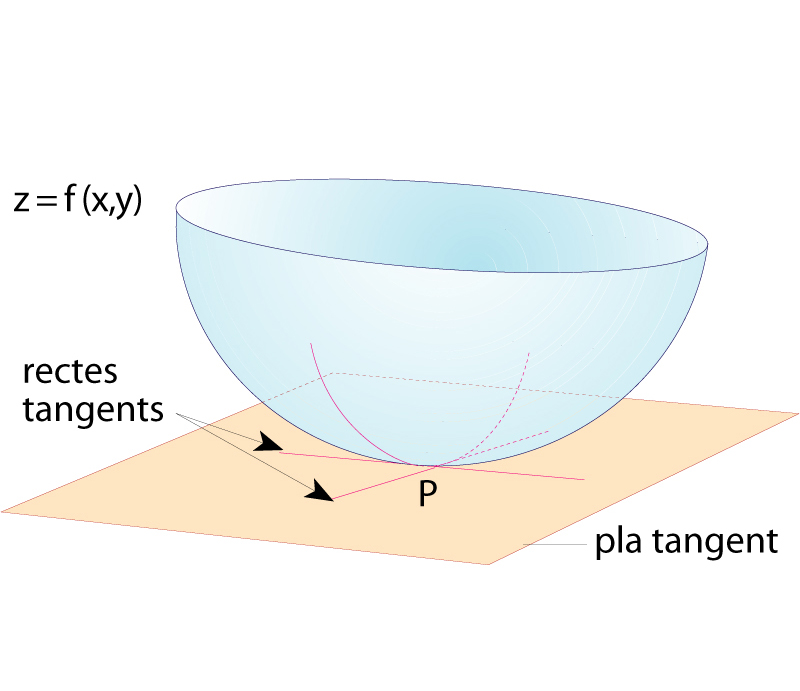
Pla tangent i dues rectes tangents a la superfície z=f(x,y) en el punt P
© Fototeca.cat
Matemàtiques
Funció tg: →-{π/2+kπ, k ∈ℤ} →ℝ, definida per l’assignació x
→tg x
, on tg x
és la tangent de l’angle que fa x
radiants.
És una funció periòdica de període 2 i el seu recorregut és -∞, ∞ És una de les sis funcions trigonomètriques o circulars i està relacionada amb les funcions sinus i cosinus per l’expressió tg x =sin x /cos x És indefinidament derivable i el seu desenvolupament en sèrie entera és quan x 2
trigonometria

1, circumferència de referència per a la definició de les raons trigonomètriques; 2, representació gràfica de les línies trigonomètriques; 3, símbols emprats en la resuloció de triangles
© fototeca.cat
Matemàtiques
Part de la matemàtica inicialment dedicada a l’estudi de les relacions entre les amplituds dels angles i les longituds dels segments que llurs costats determinen en les rectes que tallen.
La trigonometria es basa en les propietats de les anomenades raons trigonomètriques , que són definides a partir d’un punt P x,y d’una circumferència de centre O i per l’angle α que forma el radi r = OP amb l’eix OX , mitjançant els sis quocients següents sin α = y/r sinus cos α = x/r cosinus tg α = y/x tangent cotg α x/y cotangent sec α = r/x secant cosec α = r/y cosecant Quan el punt P és a una distància r = 1 de l’origen O , el valor absolut d’aquestes raons és representat per la longitud de certs segments anomenats línies trigonomètriques , respectivament, fàcils de traçar A partir de…