Resultats de la cerca
Es mostren 11 resultats
rang
Matemàtiques
Conjunt de valors que pren una determinada funció; és anomenat també abast o recorregut
.
rang d’una matriu
Matemàtiques
Ordre del més gran determinant no nul extret d’ella.
Així, si la matriu és n × n i no singular, el seu rang és n
rang d’una aplicació lineal
Matemàtiques
Rang de qualsevol matriu que representi l’aplicació.
És la dimensió del més gran subespai de l’espai de partida en el qual la restricció és bijectiva
teorema de Rouché-Frobenius
Matemàtiques
Teorema que permet la classificació dels sistemes lineals d’equacions.
Donat un sistema no homogeni de m equacions lineals amb n incògnites, escrit en forma matricial A x = b , b ≠ 0 , on A és la matriu de coeficients del sistema, b la columna dels termes independents i x la columna de les incògnites, el sistema és compatible és a dir, que té solucions si el rang de A és igual al rang de la matriu ampliada A , b matriu Si aquest rang és igual al nombre d’incògnites, aleshores es tracta d’un sistema compatible determinat o sia, amb solució única, però si el rang és menor que el nombre d’incògnites, es tracta…
mètode de racionalització de Gauss
Matemàtiques
Algorisme emprat en l’estudi dels espais vectorials que, donats uns vectors arbitraris, permet de deduir-ne efectivament els que són linealment independents i que, per tant, també són base del subespai que generen.
Hom aplica aquest mètode per a trobar el rang d’una matriu qualsevol no necessàriament quadrada, considerant cada fila de la matriu com un vector
signatura
Matemàtiques
Nombre de termes positius en una forma quadràtica reduïda a una suma de quadrats mitjançant una transformació lineal.
La signatura d’una matriu simètrica és el nombre de termes positius que apareixen en diagonalitzar la matriu Amb el rang , la signatura constitueix un dels invariants fonamentals en la classificació de les matrius corresponents a les còniques i a les quàdriques
cònica
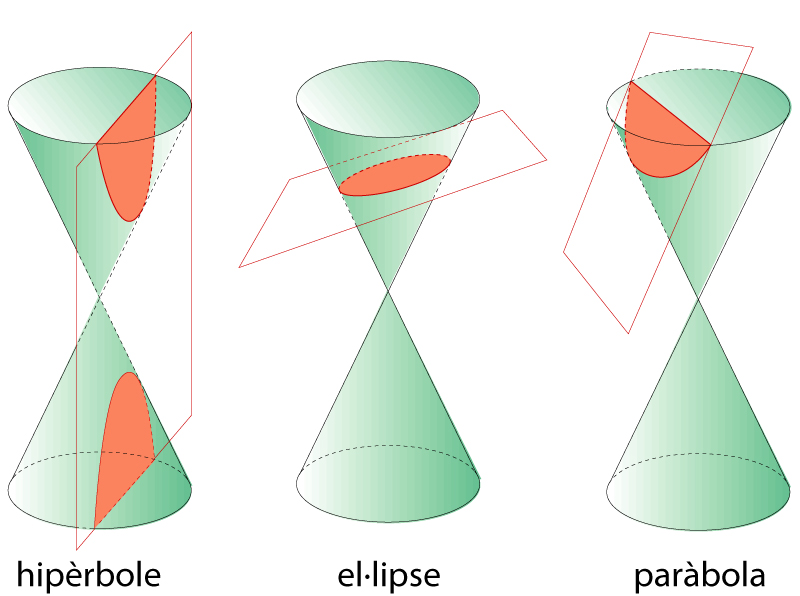
Còniques com a secció de cons
© Fototeca.cat
Matemàtiques
Corba de segon grau en un pla.
El primer estudi conegut sobre còniques és el tractat d’Apolloni de Perge, que les definia com a possibles seccions d’un con Projectivament, hom defineix la cònica com a lloc geomètric dels punts dobles d’una polaritat L’estudi afí de les còniques destaca els següents elements centre , que és el pol de la recta de l’infinit, diàmetre , qualsevol recta que passa pel centre, asímptotes , els diàmetres tangents a la cònica En l’estudi euclidià hom distingeix, a més, els eixos principals, que són una parella de diàmetres perpendiculars i també conjugats respecte a la polaritat induïda per la…
funció
Matemàtiques
Aplicació.
Segons els casos, hom fa ús d’un o de l’altre dels dos sinònims, funció o aplicació així, hom parla d’aplicació entre conjunts no numèrics o d’aplicació injectiva, però de funció entre conjunts numèrics o de funció derivable El concepte de funció és un dels conceptes fonamentals de la matemàtica Una funció entre dos conjunts A i B és representada per la notació fA →B A és el domini de definició o el camp d’existència de f , i el subconjunt de B format per les imatges dels elements de A , denotat per f A , és la imatge , abast, rang o recorregut de f Si x representa un element…
matriu
Matemàtiques
Disposició dels elements d’un cos K
de la manera següent
.
Segons que el cos K sigui el dels nombres reals o el dels nombres complexos, hom parla de matriu real o de matriu complexa , respectivament Cadascuna de les línies horitzontals de nombres és una fila de la matriu, i cada línia vertical de nombres n'és una columna En l’exemple donat, la matriu A té files i columnes hom diu que A és una matriu m × n El conjunt de les matrius m ×és notat per M m X n K Una matriu pot ésser expressada també mitjançant el seu element genèric a i j , en la forma A = a i j Aquí, és l' índex de fila i j és l' índex de columna La fila formada pels elements a i…