Resultats de la cerca
Es mostren 16 resultats
políedre
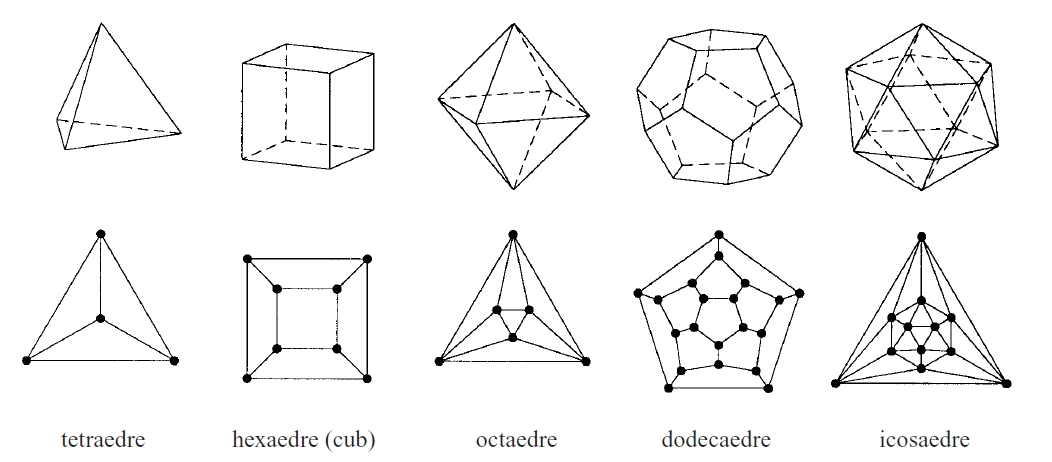
Els cinc políedres regulars i els diagrames de Schlegel associats
© Fototeca.cat
Matemàtiques
Sòlid limitat per quatre o més polígons anomenats cares.
Les interseccions de les cares constitueixen les arestes , i les interseccions de les arestes, els vèrtexs Un políedre és convex si qualsevol secció plana del políedre és un polígon convex Un políedre és còncau si no és convex Un políedre és simple si és topològicament equivalent a una esfera, és a dir, si no té forats Un políedre és regular si té les cares iguals i els angles iguals, essent les cares polígons regulars Des de la Grècia antiga hom sap que existeixen solament cinc políedres regulars el tetràedre regular , l’ hexàedre regular o cub, l’ octàedre regular , el dodecàedre regular i…
políedre estelat
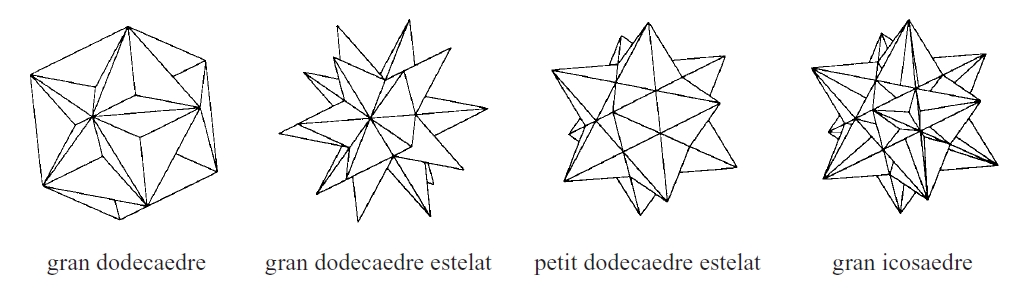
Els quatre políedres estelats regulars
Matemàtiques
Políedre que s’obté de col·locar piràmides sobre les cares d’un políedre convex o de prolongar-ne les cares.
mosaic
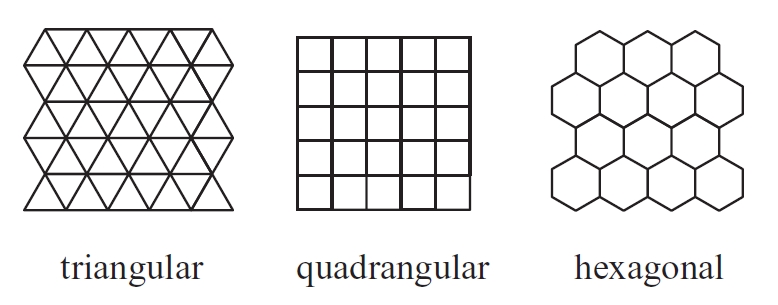
mosaics
© Fototeca.cat
Matemàtiques
Recobriment del pla per repetició d’un mòdul fix segons dues direccions.
Els mosaics regulars s’obtenen per repetició d’un polígon regular Els mosaics semiregulars es generen en combinar dos tipus de polígons regulars de dimensions convenients per al seu acoblament Únicament hi ha tres tipus de mosaics regulars i vuit de semiregulars Els únics mosaics regulars que es poden construir al pla són el triangular, el quadrangular i l’hexagonal
piramidat | piramidada
Matemàtiques
Dit dels políedres les cares dels quals són piràmides regulars.
proporció divina
Matemàtiques
Proporció a/b
=Φ, on Φ és el nombre d’or
.
Aquesta proporció ha estat emprada al llarg de la història de la geometria i de l’arquitectura Pacioli, Leonardo da Vinci, etc, puix que té relació amb molts problemes de les figures geomètriques regulars principals pentàgons, decàgons, etc
dipiràmide
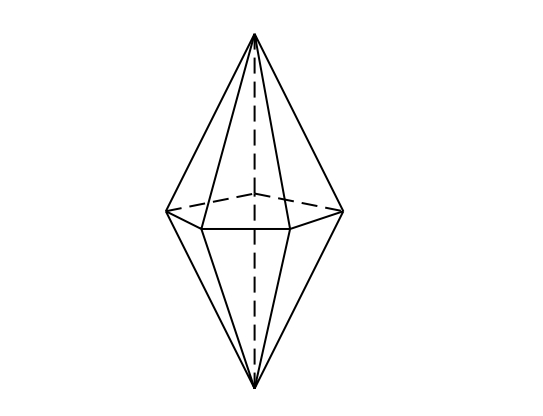
dipiràmide pentagonal
Matemàtiques
Políedre que resulta de soldar, per la base, dues piràmides de bases idèntiques.
S’anomena dipiràmide pentagonal al polídere resultat de soldar dues piràmides pentagonals per les seves bases si les piràmides són regulars, és un deltaedre de deu cares S’anomena dipiràmide triangular al políedre que resulta de soldar dues piràmides triangulars per les seves bases
Aristeu de Crotona
Matemàtiques
Matemàtic grec.
Escriví cinc llibres sobre Els llocs sòlids on formulà teoremes sobre els cinc sòlids regulars i sobre les corbes còniques Influí sobre Euclides, bé que el tractat d’Aristeu és més important i original Les seves obres només són conegudes per referències de Pappus i Euclides Això fa que tota l’originalitat de l’estudi de les còniques recaigui sobre Apolloni de Perge
autòmat finit indeterminista
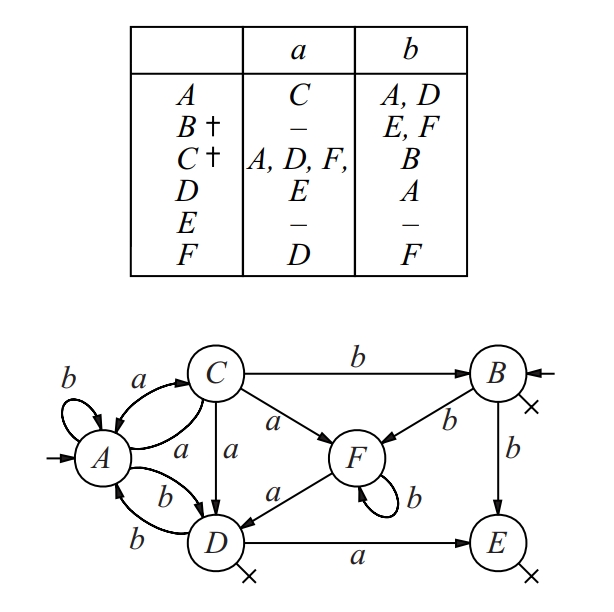
autòmat finit indeterminista
Matemàtiques
Estructura de la forma M = (Q, ∑, δ, I, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet anomenat d’entrada; δ : 2Q ⨉ ∑* → 2Q és la funció de transició que satisfà ∀P1, P2 ⊂ Q, ∀x, y∈∑*: δ(∅, x) = ∅, δ(P1, λ) = P1, δ(P1 ∪ P2, x) = δ(P1, x) ∪ δ(P2, x), δ(P1, xy) = δ(δ(P1, x)y), essent xy la concatenació de x i de y i ∑* el conjunt de paraules; I ⊂ Q és el conjunt d’estats inicial; F ⊂ Q és el conjunt d’estats finals o acceptadors.
Usualment un autòmat finit indeterminista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si q j ∈ δ q i , a S’indiquen els esstats inicials amb fletxes i els finals amb una creu Els llenguatges acceptats pels autòmats finits indeterministes són els mateixos que els reconeguts pels finits deterministes regulars L’avantatge dels indeterministes enfront dels deterministes és la facilitat de maneig i de construcció
nombres de Fermat
Matemàtiques
Nombres, Fn, definits per l’expressió (per a n = 1,2,3,...).
El 1640 Fermat cregué que aquests nombres eren primers, però l’any 1740 Euler donà una descomposició per a F 5 = 4 294 967 297, com a producte de 641 per 6 700 417, i posteriorment hom ha demostrat que per a n tal que 5 ≤n≤17 , F n no és primer, i que d’altres nombres de Fermat, com F 1 9 4 5 , F 3 3 1 0 i F 6 5 3 7 són descomponibles El 1796 Gauss demostrà que els únics polígons regulars que hom pot construir amb regle i compàs són els que tenen un nombre de Fermat de costats