Resultats de la cerca
Es mostren 111 resultats
relació
Matemàtiques
Lligam entre diversos elements d’un conjunt.
Per tal de precisar aquesta idea intuïtiva, hom defineix la relació com a qualsevol subconjunt d’un producte cartesià del conjunt amb ell mateix és a dir, que els elements són relacionats si formen un element del subconjunt En general, en una relació intervé un nombre determinat d’elements n així, una relació d’ordre entre els elements és un subconjunt del producte de n conjunts A El tipus de relació més freqüent és aquella en què n = 2, anomenada relació binària , que és un subconjunt de A × A Si els dos elements són a i b…
relació transitiva
Matemàtiques
Relació R en un conjunt A tal, que si a i b són relacionats per R (a R b) i b, c també ho són (b R c), aleshores entre a i c també hi ha la mateixa relació.
Les relacions numèriques d’igualtat o la relació “ésser multiple de” són transitives Les relacions d’equivalència i ordre també ho són Relacions com la d’"ésser amic” o “ésser pare de”, per contra, no ho compleixen Tota relació transitiva i reflexiva tot element és relacionat amb ell mateix, a R a és dita preordre
relació reflexiva
Matemàtiques
Relació binària R que compleix que, per a tot element a del conjunt A en el qual és definida, a R a.
Un exemple de relació reflexiva és el constituït pel parallelisme de rectes en canvi, no ho és la perpendicularitat
relació binària
Matemàtiques
Condició relativa a dos elements d’un conjunt que és satisfeta per determinats parells d’elements (eventualment per tots o per cap parell).
Sovint hom representa una relació binària per una taula de doble entrada on són assenyalats els quadres corresponents als parells que satisfan la relació La taula següent dóna la relació a és múltiple de b entre els nombres del conjunt 1,2,3,4,5,6 Entre les relacions binàries sobresurten per llur importància les relacions d’equivalència i les relacions d’ordre
relació antisimètrica
Matemàtiques
Relació binària establerta entre els elements d’un conjunt C tal que si per a qualsevol parella d’elements, a i b, s’acompleix queaRb (a és relacionat amb b) i bRa aleshores a = b, i a l’inrevés.
És a dir
relació d’ordre
Matemàtiques
Relació binària R entre els elements d’un conjunt C que és reflexiva, antisimètrica i transitiva.
La parella C, R constitueix un conjunt ordenat És usual la notació ≤per a designar la relació d’ordre desigualtat 5, i a ≤ b és llegit '' a menor o igual a b' , o bé '' a inferior a b' aquesta notació generalitza la coneguda i usual relació “ésser menor que o igual a” que ordena els nombres Unes altres relacions d’ordre importants són la relació d’igualtat, la relació d’inclusió entre conjunts, la relació “ésser divisor de” en els nombres naturals, etc En un conjunt ordenat, són elements notables el màxim , el mínim , el…
relació de proximitat
Matemàtiques
Relació binària S entre els subconjunts d’un conjunt E, que fou introduïda per Efremovič per tal de generalitzar la relació ‘‘ésser pròxim’’ que hom utilitza correntment en l’espai mètric ordinari.
La relació de proximitat és definida pels axiomes següents ASB ⇔ BSA , és a dir, la relació S és simètrica ASB ⇒ A ≠∅i B ≠∅, és a dir, el conjunt buit no és pròxim a cap altre AS B ∪C ⇒ ASB o ASC , és a dir, un conjunt és pròxim a la reunió de dos conjunts si és pròxim, almenys, a un d’ells A ∩B ≠∅⇒ASB , és a dir, dos conjunts que es tallen són pròxims { X } S { Y } ⇔ X=Y , és a dir, un punt només és pròxim a si mateix si A$B aleshores existeix un conjunt C tal que B$C i A$C c , on C c és el conjunt complementari de C Tota proximitat indueix una topologia prenent…
relació d’equivalència
Matemàtiques
Relació binària entre els elements d’un conjunt que permet d’establir una classificació d’aquests elements de tal manera que resti cadascun en una classe, dita d’equivalència, i aquestes classes no tinguin cap element comú.
Perquè una relació sigui d’equivalència cal que sigui reflexiva, simètrica i transitiva relació Tota relació d’equivalència estableix una classificació del conjunt i tota classificació determina una relació d’equivalència Són equivalents dos elements que pertanyen a la mateixa classe El conjunt de les classes considerada cadascuna com un nou element és anomenat conjunt quocient del conjunt de partida C per a aquesta relació R , i s’escriu C/R Una aplicació d’un conjunt en un altre determina una relació d’…
relació de pertinença
Matemàtiques
Relació que determina els elements que pertanyen a un conjunt
.
corbes de Lissajous
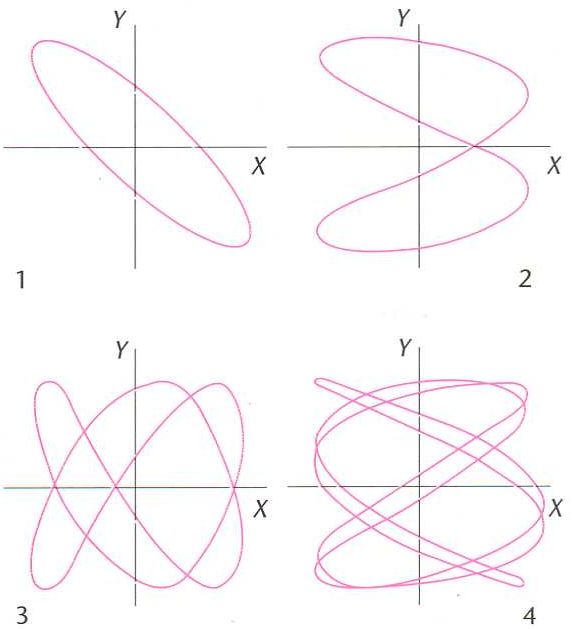
Corbes de Lissajous la relació entre les pulsacions wx i wy dels dos moviments corresponents.
© Fototeca.cat
Matemàtiques
Corbes que apareixen en la composició de dos moviments vibratoris harmònics perpendiculars entre ells.
Hom obté corbes molt diverses, en general obertes, però, si la relació entre els períodes dels dos moviments és racional, la corba obtinguda és tancada i el moviment resultant és periòdic si els dos períodes són iguals, la corba resultant és una circumferència o una ellipse Hom les pot reproduir fàcilment en un oscilloscopi fent que les tensions horitzontal i vertical siguin sinusoidals
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina