Resultats de la cerca
Es mostren 13 resultats
conjunt recursiu
Matemàtiques
Conjunt X
en la seva funció característica 1 x
és recursiva o computable.
Dit més informalment, un conjunt X és recursiu quan existeix un algorisme que permet de decidir la resposta a la pregunta ' x ∈ X'
problema de Dido
Matemàtiques
Problema consistent en la determinació de quina d’entre totes les corbes tancades sense punt doble, amb un perímetre donat, conté l’àrea més gran.
Fou resolt per J Bernoulli, que deduí correctament que la resposta és la circumferència el nom és atribuït llegendàriament a la fundadora de Cartago, que l’hauria plantejat empíricament
anàlisi de la variància
Matemàtiques
Qualsevol de les tècniques utilitzades per a determinar la variància observada entre diferents conjunts de dades, especialment per a determinar si les diferències entre dues o més mostres poden ser explicades com a variacions degudes a l’atzar dins una mateixa població.
L’anàlisi de la variància és un procediment creat per RA Fisher per a descompondre la variabilitat d’un experiment en components generalment independents que puguin assignar-se a diferents causes, per a avaluar la influència d’aquestes causes en la variable resposta
problema diofàntic
Matemàtiques
Un dels 23 problemes que David Hilbert plantejà l’any 1900 al Congrés Internacional de Matemàtiques com a problemes que caldria resoldre durant el segle XX.
Segons aquest, donat un polinomi amb coeficients sencers, de grau i nombre d’incògnites arbitraris i tots nuls llevat d’un nombre finit, hi ha un algorisme que permeti de decidir si té solució sencera La resposta negativa fou donada finalment pel matemàtic rus Iurij Matijasevicz l’any 1970
conjectures de Burnside
Matemàtiques
Conjunt de problemes algèbrics relatius als grups, plantejats per W.S.Burnside.
D’una banda, es preguntà si tot grup engendrat per un nombre finit d’elements i en el qual tot element és d’ordre finit és necessàriament finit aquesta conjectura fou resposta negativament per Novikov el 1959 D’altra banda, demostrà que si p i q són enters primers diferents, aleshores tot grup d’ordre p 2 q és grup resoluble
problema dels set ponts de Königsberg
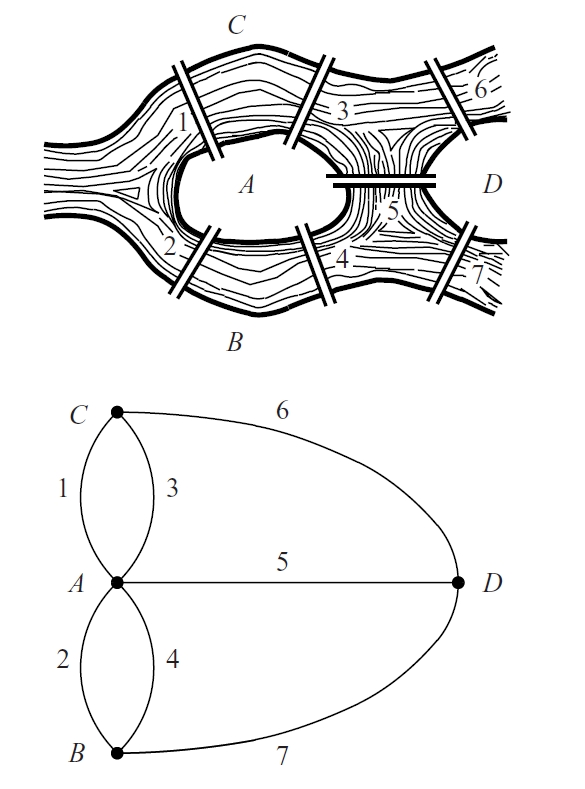
problema dels set ponts de Königsberg
Fototeca.cat
Matemàtiques
Problema la solució del qual s’associa sovint amb l’origen de la teoria de grafs.
La ciutat prussiana de Königsberg actualment Kaliningrad està dividida pel riu Pregol’a, que voreja l’illa de Kneiphof Hi havia set ponts disposats com s’indica a la figura Els habitants de la ciutat es plantejaven si era possible fer un recorregut tancat que passés una sola vegada per cadascun dels set ponts En llenguatge de teoria de grafs, la pregunta és si el graf és eulerià La resposta és negativa La solució del problema va ser trobada per Leonard Euler, el 1736, introduint per primer cop la noció de graf i resolent a la vegada un problema de caràcter més general
problema de les paraules
Matemàtiques
Problema d'àlgebra.
D’una banda si hom disposa d’un alfabet finit OOO = {a 1 ,,a n } i, per concatenació, construeix els mots M = ζ 1 ζ r , on cada símbol ζ i és una de les lletres a j ∈ OOO d’aquest alfabet i r ∈ ℕ si, d’altra banda, hom disposa d’un cert diccionari que estableix l’equivalència de certes parelles de mots i, finalment, hom accepta el fet que, en substituir en un mot M = M 1 mM 2 un cert sumbmot m per un altre mot m´ equivalent, obté un mot equivalent M´ = M 1 m' M 2 Cal plantejar la pregunta següent donats dos mots arbitraris M i N , hi ha algun algorisme que permeti de decidir si són…
Oliba
Música
Cristianisme
Matemàtiques
Monjo de Ripoll, matemàtic, músic i poeta, deixeble del bisbe i abat homònim.
Se’n conserven dos opuscles en els quals discuteix el dia del naixement de Jesús, dedicats a l’abat Oliba, el 1037, i al monjo Dalmau, company seu, el 1065, dades extremes de la seva activitat coneguda, i una altra obreta sobre el cicle pasqual de Dionís En el camp de les matemàtiques escriví sobre la multiplicació i la divisió del nombre de l’àbac i un altre tractat, que li és atribuït, sobre pesos i mesures L’obra més important, però, és el recull de teòrics musicals antics que formen el Breviarium de musica , amb un pròleg en vers adreçat al monjo Pere, futur abat de Ripoll,…
,
teoria de la computació
Matemàtiques
Branca de les matemàtiques que estudia problemes de decidibilitat.
Com és usual en la història de les matemàtiques, té orígens aparentment molt diferents que finalment conflueixen i permeten d’establir el que esdevé una teoria enormement potent i irrenunciable Cal remarcar-ne el problema diofàntic plantejat per David Hilbert l’any 1900, i el problema de les paraules que sorgí en el món de la topologia algèbrica Es tracta de dos problemes típics de decidibilitat és a dir, aquells en què cal disposar d’un mètode que permeti de decidir una o altra de dues opcions atesa una equació diofàntica, té solució, són equivalents dues paraules donades per endavant L’any…
teoria de nombres
Matemàtiques
Part de la matemàtica que estudia les relacions entre els nombres enters.
En la història de la teoria de nombres hom pot assenyalar dos grans períodes un que va des d’Euclides fins a Hilbert, i un altre que comença a partir de Hilbert Els primers tractats de teoria de nombres es troben en els Elements d’Euclides i en l' Aritmètica de Diofant d’Alexandria, i tracten, respectivament, de la divisibilitat en els racionals enters i de l’obtenció de solucions racionals i enteres d’algunes equacions algèbriques La figura més coneguda d’aquesta primera etapa és la del matemàtic francès Pierre de Fermat 1601-65, que conjecturà el famós gran teorema de Fermat encara avui no…