Resultats de la cerca
Es mostren 9 resultats
lemniscata
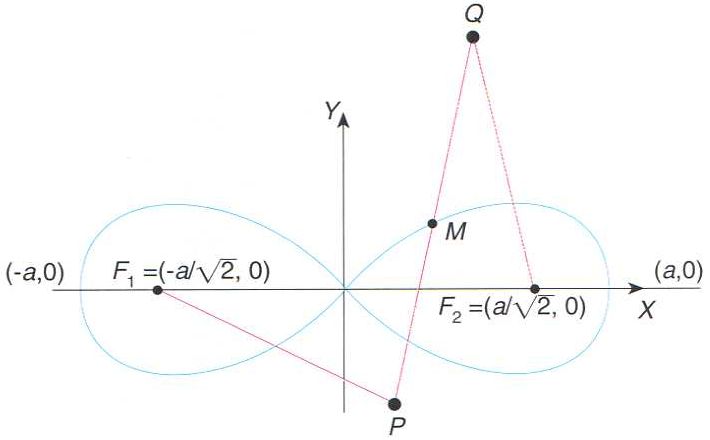
Contrucció geomètrica de lemniscata: ès el lloc geomètric dels punts M situats al mig d’un segment de longuitud constant, que uneixen dos punts, P i Q, que descriuen circumferències de radis a i de centres en el focus F1 i F2
© Fototeca.cat
Matemàtiques
Corba algèbrica de quart grau que té una forma semblant a la d’un vuit.
És coneguda també com a lemniscata de Bernoulli , i pot ésser expressada per l’equació x 2 + y 2 2 = a 2 x 2 - y 2
pla | plana
perspectiva cònica
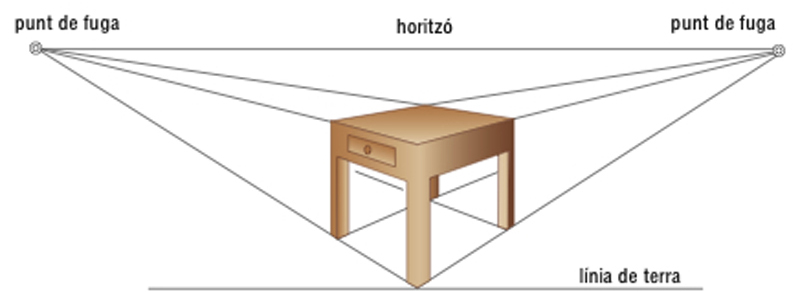
Representació d’una taula en perspectiva cònica obliqua (dos punts de fuga)
© Fototeca.cat
Art
Disseny i arts gràfiques
Matemàtiques
Perspectiva central el centre de projecció o pol de la qual és l’ull de l’observador.
Per al traçat d’aquesta perspectiva, hom admet que la llum que arriba a l’ull procedent de qualsevol punt d’un objecte és una línia recta, que rep el nom de raig visual Els principals elements per al seu traçat són la posició de l’ull o punt de vista , de la qual depèn l’efecte de la perspectiva l' horitzó o la línia horitzontal traçada en el pla del quadre, a l’alçada del punt de vista, que ocupa en el quadre la mateixa posició que la perspectiva de l’horitzó natural el pla geometral , que és el pla perpendicular al pla del quadre i on hom suposa que són situats l’observador i…
diagonal
Matemàtiques
Segment d’una recta que uneix dos vèrtex d’un políedre no situats a la mateixa cara.
superfície esfèrica
Matemàtiques
Superfície constituïda per tots els punts de l’espai que són a una distància (radi) fixa d’un punt fix (centre).
L’estudi de les figures que es poden traçar damunt una superfície esfèrica dóna lloc a la geometria esfèrica En són els elements fonamentals els punts i les circumferències màximes situades en plans que passen pel centre Figures importants són els triangles esfèrics , amb els quals hom pot fer càlculs per mitjà de la trigonometria esfèrica, que guarden un cert parallelisme amb els de la trigonometria plana La geometria esfèrica ha tingut un gran desenvolupament pel fet que la cosmografia estudia la posició dels astres com si fossin punts situats sobre una esfera de radi infinit i…
arc capaç
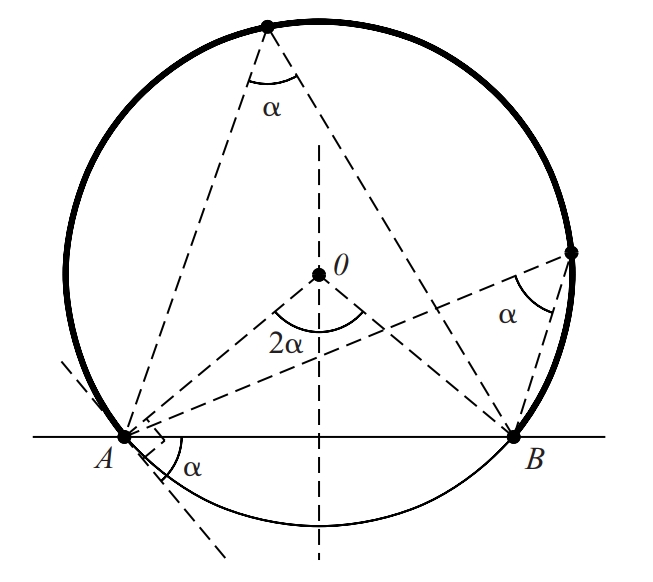
Arc capaç del segment AB per a l’angle α.
© fototeca.cat
Matemàtiques
Lloc geomètric dels punts
d’un pla que, situats en un mateix semiplà respecte d’una recta donada, formen un mateix angle prefixat amb els extrems d’un segment d’aquesta recta.
És un arc circular amb extrems coincidents amb els del segment i es pot considerar una corba isotòpica associada a aquest segment
obert | oberta
Matemàtiques
En un espai mètric E, dit del conjunt C tal, que donat un punt qualsevol a de C existeix una distància d tal, que tots els punts de E situats a una distància del punt a inferior a d pertanyen al conjunt C.
Així, entre els intervals de la recta real, els únics oberts són els intervals oberts interval Les propietats formals dels conjunts oberts han conduït a la formulació de l’anomenada topologia general , en la qual la noció d’obert és una noció primitiva que només és subjecta als tres axiomes següents el conjunt buit és obert, tota unió de conjunts oberts és un conjunt obert, i tota intersecció finita de conjunts oberts és un conjunt obert
inscriure
Matemàtiques
Traçar (un polígon) a l’interior d’un altre polígon, o bé (un políedre) a l’interior d’un altre políedre, de manera que els vèrtexs del primer polígon o políedre siguin situats sobre els costats o les cares del segon polígon o políedre, respectivament.
inscriure
Matemàtiques
Traçar (un polígon) a l’interior d’una corba, o bé (un políedre) a l’interior d’una superfície, de manera que tots els vèrtexs del polígon o del políedre siguin situats sobre la corba o la superfície sigui tangent a totes les cares del políedre, respectivament.