Resultats de la cerca
Es mostren 221 resultats
conjunt ben ordenat
Matemàtiques
Conjunt ordenat en el qual tot subconjunt no buit té un primer element.
Conjunt ordenat OOO X ,≤OOO si, i només si, tot subconjunt Y ⊆ X , no buit, té primer element Els nombres ordinals mesuren precisament les diferents menes de bons ordres possibles És a dir, tot conjunt ben ordenat és ordre-isomorf a un únic nombre ordinal
subconjunt
Matemàtiques
Qualsevol conjunt contingut en un altre conjunt, és a dir, que tot element d’aquest ho és d’un altre.
Un subconjunt és una part d’un conjunt Si A és un subconjunt de B, hom ho representa així A⊆B La negació de A⊆B és representada per A⊄B El símbol ⊆és anomenat d’inclusió Tot conjunt admet els subconjunts trivials ell mateix i el conjunt buit ø La collecció de subconjunts d’un conjunt donat A forma un altre conjunt, dit conjunt de les parts de A , que hom representa per P A, i, per tant, PA = {BB⊆A} Si té n elements, PA en té 2 n
aplicació
fototeca.cat
©
Matemàtiques
correspondència
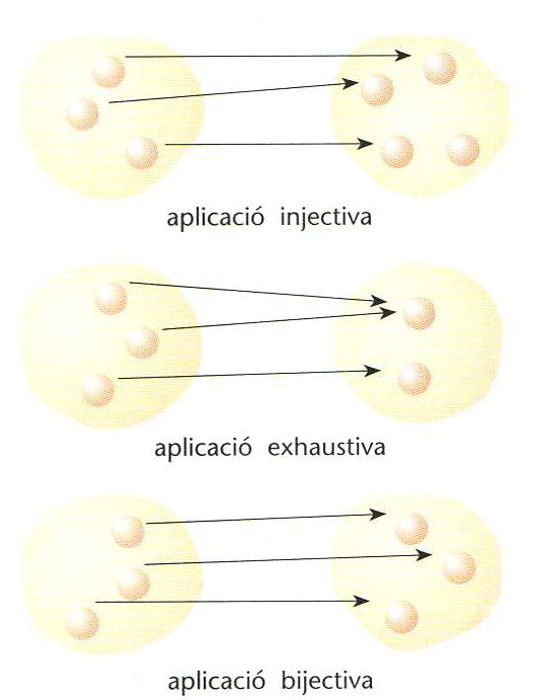
entre dos conjunts en què tot element del primer conjunt (o original) té una imatge i una de sola en el segon conjunt.
Si elements diferents tenen imatges diferents, l’aplicació és dita injectiva si tot element del segon conjunt és imatge d’un element almenys del primer, l’aplicació és exhaustiva una aplicació que sigui alhora injectiva i exhaustiva és dita bijectiva o unívoca
separable
Matemàtiques
Dit d’un espai topològic que conté un subconjunt numerable que és dens, és a dir, que tot entorn d’un punt qualsevol de l’espai conté almenys un punt del subconjunt numerable.
La recta real ℝ és separable perquè existeix el subconjunt numerable i dens dels racionals ℚ Tot espai topològic que satisfà el segon axioma de numerabilitat és separable en particular, ho és tot espai de Hilbert
grup resoluble
Matemàtiques
Grup on tot factor de composició és abelià.
Segons la teoria de Galois, una equació és resoluble per radicals si, i només si, el seu grup de Galois és resoluble cos 8
funció doblement periòdica
Matemàtiques
Funció f:ℂ→ℂtal que existeixen dos complexos no nuls, z1 i z2, anomenats períodes, que satisfan z1≠az2 per a tot a∈, i tals que f(z+n1z1 +n2z2 )=f(z).
per a tot parell d’enters n 1 i n 2 i per a tot complex z
funció còncava
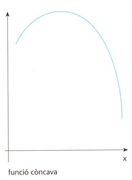
Funció concàva
© Fototeca.cat
Matemàtiques
Funció f:(a,b)⊂ℝ→ℝtal que per a tot α∈(0,1) se satisfà f(αx+(1—α)y)≥αf(x)+(1—α)f(y), on a<x<b i a<y<b.
El significat geomètric és que per a tot interval x,y ⊂ a,b la corda que uneix f x amb f y és situada per sota de l’arc que uneix f x amb f y
funció convexa
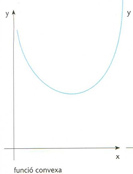
Funció convexa
© Fototeca.cat
Matemàtiques
Funció f:(a,b)⊂ℝ→ℝtal que per a tot α∈(0,1) se satisfà f(αx+(1-α)y)≤αf(x)+1-α)f(y), on a<x<b i a<y<b.
El significat geomètric és que per a tot interval x,y ⊂ a,b la corda que uneix f x amb f y és situada per sobre de l’arc que uneix f x amb f y
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina