Resultats de la cerca
Es mostren 40 resultats
transformació
Matemàtiques
Aplicació bijectiva d’un conjunt en un altre o en ell mateix.
El conjunt de les transformacions d’un conjunt en ell mateix té estructura de grup respecte a la composició de transformacions la composició en el sentit d’aplicar successivament de manera ordenada dues transformacions és anomenada també producte Segons la definició de Felix Klein, la geometria és l’estudi de les nocions invariants per a un grup de transformacions geometria Com a exemples de transformacions en el pla poden ésser esmentades les rotacions, les simetries axials, les translacions, etc i en l’espai, les simetries respecte a un eix o a un pla, les rotacions axials,…
transformació integral
Matemàtiques
Operació mitjançant la qual una funció f(x) és transformada en una altra funció F(y) gràcies a relacions de tipus integral.
L’exemple més senzill és la simple integració F y = ∫ a y f x dx Una expressió vàlida per a un nombre important de transformacions integrals és F y = ∫ a b K x,y f x dx en la qual K x,y rep el nom de nucli i caracteritza l’esmentada transformació en molts casos, els límits d’integració són 0, ∞ i -∞, ∞ Cal esmentar, com a exemples importants, la integral ponderada, la integral de convolució, la transformada de Fourier anàlisi de Fourier, la de Laplace, la de Kankel, i la de Mellin
transformació simètrica
Matemàtiques
Transformació T d’un espai euclidià E tal que Tx·y = x·Ty si · indica el producte escalar de E.
transformació lineal
Matemàtiques
Transformació L que satisfà la propietat de linealitat és a dir, tal que L(αv+ w)=αL( v)+ L( W)
.
transformació d’igualtat
Matemàtiques
Transformació geomètrica bijectiva que conserva la distància entre els punts.
afinitat
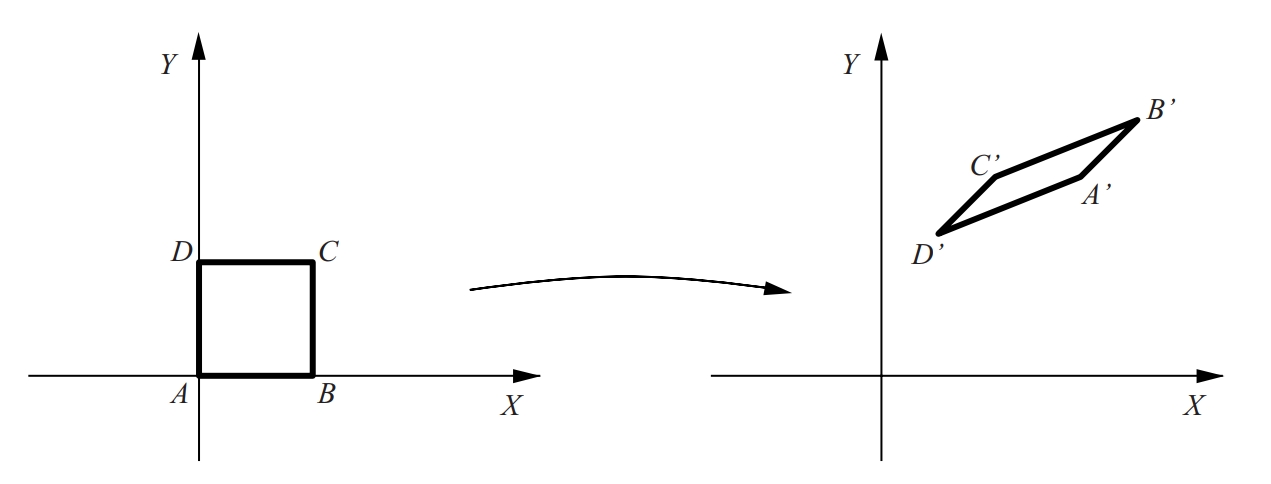
afinitat Transformació afí d’un quadrat
© Fototeca.cat
Matemàtiques
Transformació de l’espai afí en si mateix, que fa correspondre línies paral·leles amb línies paral·leles, punts propis amb punts propis i no canvia el subespai de l’infinit.
Enclou, entre d’altres transformacions, la traslació, la rotació i la simetria Les propietats geomètriques conservades per aquesta transformació són dites afins o lineals llur estudi constitueix la geometria afí
homotècia
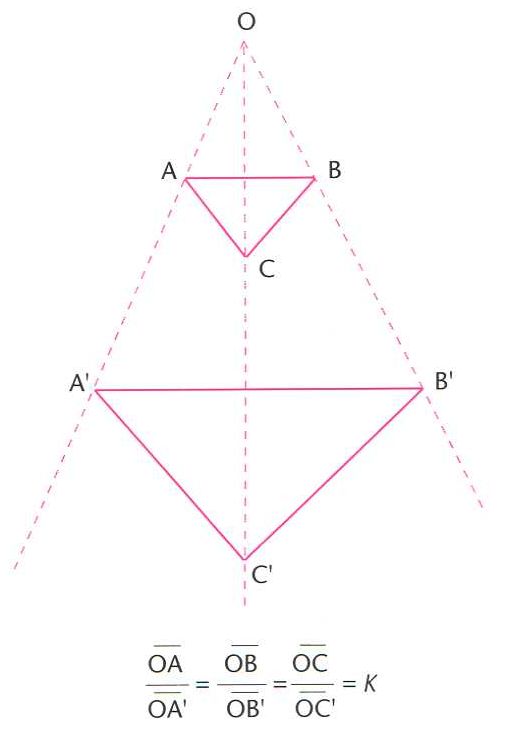
Homotècia, transformació homotètica d’un triangle ABC (O, centre de l’homotècia; k, raó d’homotècia)
© Fototeca.cat
Matemàtiques
Transformació geomètrica del pla o de l’espai que compleix aquestes dues condicions.
Qualsevol punt A i la seva imatge A' són alineats amb un punt fix O anomenat centre d’homotècia , i els segments compleixen la relació k essent, per a cada homotècia, una constant real anomenada raó de l’homotècia Les homotècies transformen rectes en rectes, circumferències en circumferències i conserven els angles
topologia

Topologia Les figures unides amb fletxes són topològicament iguals, perquè és possilbe passar de l’una a l’altra per mitjà d’una transformació contínua
© Fototeca.cat
Matemàtiques
Part de la matemàtica que estudia aquelles propietats dels conjunts de punts de la recta, del pla, de l’espai o d’espais de dimensions superiors que no són alterades per les transformacions contínues.
Es tracta de propietats geomètriques que no depenen de cap magnitud, sinó únicament de la posició relativa dels punts Per exemple, el fet que dos punts puguin unir-se o no per un camí, o que el nombre de cares menys el d’arestes més el de vèrtexs d’un políedre esfèric sigui sempre dos teorema d’Euler Aquí hom entén per transformació contínua aquella que admet una inversa i que tant ella com la inversa són contínues L’íntima connexió que hi ha entre el concepte de continuïtat d’una funció en un punt i el d’entorn d’un punt permet de transportar l’estudi de propietats topològiques a aquells…