Resultats de la cerca
Es mostren 12 resultats
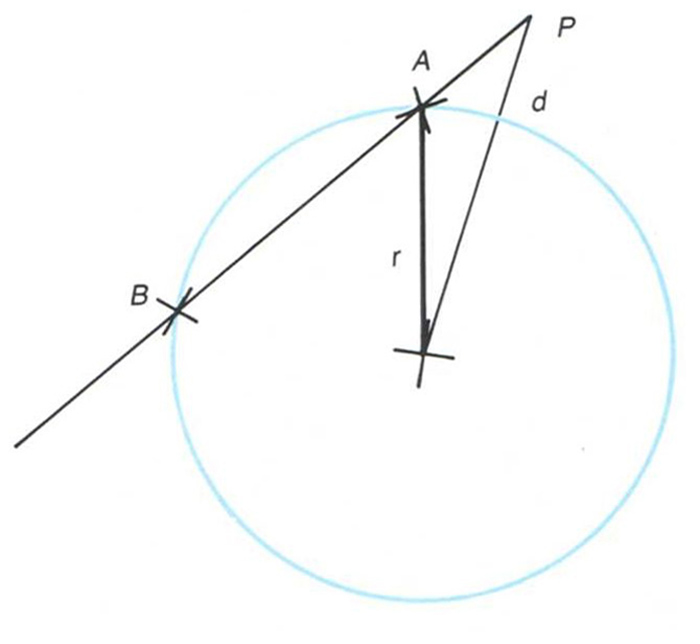
potència d’un punt respecte a una circumferència
fototeca.cat
©
Matemàtiques
Donats un punt P
i una circumferència, producte de les distàncies del punt P
als dos punts A
i B
que una recta que passa per P
determina sobre la circumferència.
Es verifica que el dit producte, és independent de la recta traçada fototecacat ©
espai afí
Matemàtiques
Caràcter d’un conjunt A
respecte a un espai vectorial E
, amb el qual hom pot definir una aplicació E
× A → A.
Es compleix que per a tot parell v , a , on v pertany a E i a pertany a A , li correspon l’element v + a de A , i que verifica les propietats L’espai afí s’estudia dins el context de la geometria analítica
postulat d’Arquimedes
Matemàtiques
Proposició segons la qual si hom pren dos elements qualssevol, α i β, d’un conjunt que tingui estructura de semigrup ordenat, existeix un nombre enter n tal que na ⩾ β, és a dir, hi ha múltiples del petit majors que el gran.
L’estructura de semigrup és la que té condicions mínimes per a poder enunciar el postulat d’Arquimedes Generalment, però, hom parla de cossos arquimedians Els conjunts en els quals es verifica aquesta proposició són anomenats conjunts arquimedians per exemple, els nombres reals i els altres conjunts no arquimedians per exemple, els nombres transfinits
espai projectiu
Matemàtiques
Conjunt de classes d’equivalència, P, de punts de Rn + 1 — {Ō}.
On R n + 1 és un espai vectorial de dimensió n + 1, obtingudes per la relació ''dos punts x i x' estan relacionats si i només si estan alineats amb l’origen’, és a dir, si es verifica x ' 1 ,, x' n + 1 = r x 1 ,, x n 1 per a tot nombre real r ≠ 0 El seu estudi pertany a la geometria projectiva
espai prehilbertià
Matemàtiques
Espai vectorial E
definit sobre el cos complex ℂ, en el qual hi ha definida una forma hermítica positiva no degenerada.
És a dir, una aplicació f E x E →ℂque verifica les condicions 1 f x + y , z = f x , z + f y , z , 2 f a x , y = a * f x , y , on a * és el conjugat de a ∈ℂ, 3 f x , x = f y , x * 4 f x , x ∈ℝ + , i 5 si f x , y = 0 per a tot y ∈ E , aleshores x = 0 El nom de prehilbertià és degut al fet que a partir d’aquest espai hom defineix l’espai de Hilbert per un procés de completació
punt fix
Matemàtiques
En una aplicació f, punt x que verifica la condició f(x) = x.
També és anomenat punt doble Per exemple, el centre de simetria és un punt doble en la simetria central Brouwer ha demostrat l’anomenat teorema del punt fix , segons el qual tota aplicació contínua en una esfera n -dimensional amb ng 2 té un punt fix El teorema té com a conseqüència que la major part de les deformacions físiques tinguin punts fixos
pla

Equació del pla
© fototeca.cat
Matemàtiques
Superfície tal que qualsevol recta que passi per dos dels seus punts es troba totalment continguda en la dita superfície.
Els plans, juntament amb els punts i les rectes, són els elements geomètrics primitius en l’axiomatització de Hilbert de la geometria D’altra banda, un pla és determinat per tres punts no alineats, o bé per dues rectes que es tallin o siguin paralleles, o bé per un punt i una recta que no contingui el punt A l’espai euclidià ℝ 3 un pla pot ésser representat per l’equació A x— x 1 + B y— y 1 + C z— z 1 = 0, en la qual x 1 , y 1 , z 1 són les tres coordenades d’un punt P 1 donat del pla, A, B, C són les tres components d’un vector N normal al pla, i x, y, z són les tres…
àlgebra

Triàngle numèric, més tard conegut com a triangle de Pascal, d’un manuscrit xinès del 1303
© Fototeca.cat
Matemàtiques
Branca de les matemàtiques que estudia les estructures algèbriques dels conjunts.
Hom l’aplica, per tant, en les situacions on hi ha un conjunt ben definit i una noció clara d’operació entre els seus elements operació interna o entre aquests i els elements d’altres conjunts operació externa L’àlgebra ha evolucionat des de l’interès inicial per a resoldre problemes fonamentalment pràctics fins al desenvolupament del mètode abstracte Dues inclinacions diferents han desembocat en l’àlgebra moderna D’una banda, l’ àlgebra clàssica , simple instrument per a fer càlculs i resoldre equacions que usava només els conceptes immediats que hom reconeixia al problema les quantitats…
espai vectorial
Matemàtiques
Grup abelià E
en el qual hi ha definida una llei de composició externa amb elements d’un cos K
, K
× E
→ E tal, que al parell (λ, e
) correspon l’element λ e
.
I acomplint-se les propietats λ + μ e = λ e + μ e , λ e + f = λ e + λ f , λμ e = λμ e i 1 e = e Els elements de E són anomenats vectors , i els elements de K , escalars Una part de E que sigui subgrup respecte a la suma i que sigui estable respecte al producte per qualsevol escalar, és anomenada subespai de E , i amb les mateixes operacions de E és un altre espai vectorial Si F és un subespai de E , hom pot definir congruències a E mitjançant la relació d’equivalència x ≡ y mòd F , si i només si la diferència x — y pertany a F Això permet de formar el conjunt quocient E/F quocient, el…
àlgebra associativa
Matemàtiques
Estructura composta (A,+,×,·) on (A,+,×) és un anell, (A,+,·) és un mòdul sobre un anell commutatiu amb unitat K i es verifica que, si λ∈K i a,b∈A, λ(ab)=a(λb)=(λa)b.
Les nocions d’àlgebra nulla, unitària, commutativa són les equivalents a les de l’anell L’àlgebra és lineal si A, +, és un espai vectorial Són importants l’àlgebra tensorial, la simètrica i l’exterior sobre un espai vectorial