Resultats de la cerca
Es mostren 15 resultats
discontinuïtat
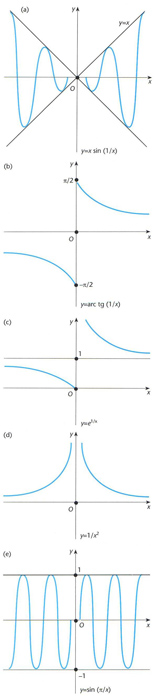
Discontinuïtat d’una funció: (a) discontinuitat evitable en x = 0, amb valor veritable y(0) = 0; (b) discontinuïtat de primera espècie infinita en x = 0, amb salt -2; (c) discontinuïtat de primera espècie infinita amb un punt d’infinit en x = 0; i (e) discontinuïtat de segona espècie finita en x = 0, per inexistència d’ambdós límits laterals quan x 0
© Fototeca.cat
Matemàtiques
Manca de continuïtat d’una funció en un punt o en un conjunt de punts, els quals són anomenats, per extensió, les discontinuïtats de la funció.
Atès que una funció f x és contínua en un punt a si i només si existeix i és igual a f a , la funció f x és discontínua en a si i només si no se satisfà alguna d’aquestes dues condicions, la qual cosa s’esdevé en els següents casos En primer lloc, pot passar que existeixi però que f a no existeixi f no sigui definida a a , o bé que aleshores, a és una discontinuïtat evitable , i la discontinuïtat és evitada redefinint el valor de f x al punt a tot assignant-li el valor el qual és anomenat valor veritable de f x en a En segon lloc, pot ocórrer que no existeixi…
demostració per recurrència
Matemàtiques
Mètode de demostració que consisteix a demostrar que una proposició és veritable per a 1 i que si és veritat per a n tamb é ho és per a n + 1.
D’això hom dedueix que la proposició és veritable per a tot n
definició per recurrència
Matemàtiques
Definició d’una funció sobre els nombres naturals definint-la per a 1 i, per a cada n més gran que 1, en funció dels valors que pren per a nombres més petits que n
.
Per exemple, la funció factorial pot ésser definida fent 1 = 1 i, per a un n > 1, fent n = n -1 n Aquests procediments de demostració i de definició, ja coneguts i emprats pels grecs, han estat generalitzats i ara hom utilitza les recurrències a qualsevol conjunt ben ordenat on tot subconjunt té mínim Aleshores, per a demostrar que una proposició és veritable per a tot element del conjunt ben ordenat, basta demostrar que és veritable per a tot element si ja ho és per a tots els anteriors
John Wallis
Matemàtiques
Matemàtic anglès.
Veritable precursor del càlcul infinitesimal, efectuà nombroses aportacions, com ara diversos desenvolupaments en sèrie, productes infinits un dels quals per al càlcul de π, les fraccions, els exponents negatius i fraccionaris, els logaritmes, la cicloide, etc Aplicà la matemàtica a la física, com, per exemple, en l’estudi que féu dels cossos inelàstics per a la Royal Society
Leonardo Torres Quevedo

Leonardo Torres Quevedo
© Fototeca.cat
Matemàtiques
Enginyer i matemàtic castellà.
Fou president de l’Academia de Ciencias de Madrid És conegut sobretot per les seves màquines automàtiques de calcular destinades especialment a resoldre equacions algèbriques i diversos dispositius per al control remot, mitjançant ones hertzianes Pot ésser considerat com un precursor del càlcul automàtic es féu cèlebre amb el seu jugador d’escacs , veritable autòmat capaç de seguir les diverses jugades possibles Construí un transportador aeri a les cascades del Niàgara i un tipus de dirigible d’estructura funicular
Pierre Gassendi
Filosofia
Física
Matemàtiques
Cristianisme
Clergue; matemàtic, físic i filòsof materialista francès.
Estudià teologia, grec i hebreu a Ais de Provença i es doctorà en teologia a Avinyó Fou professor 1645 al Collège Royal de París És conegut pels seus atacs a la filosofia dels aristotèlics, que considera com a purament verbal, car, per a ell, la veritable ciència ha de partir de les qualitats experimentals de les coses Fonamenta el coneixement en una doctrina sensualista i en l’atomisme clàssic de Demòcrit i Epicur Fou amic de Hobbes, entusiasta de Galileu, Copèrnic i Kepler i contradictor de l’intellectualisme cartesià Escriví llibres de física, matemàtiques, astronomia i…
perspectiva cavallera
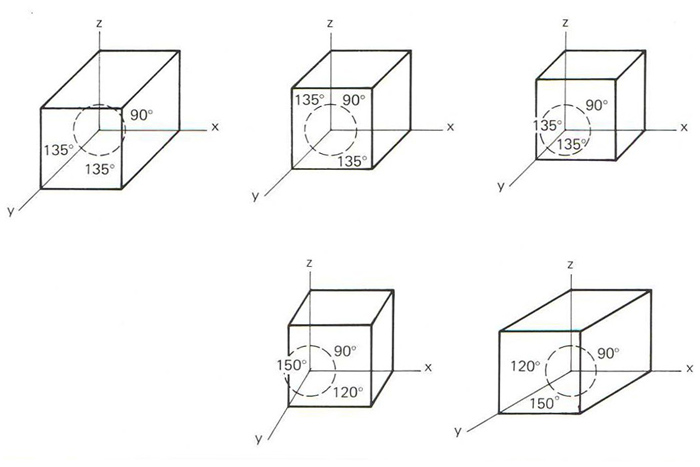
Representació d’un cub amb diferents reduccions i angles
© fototeca.cat
Art
Disseny i arts gràfiques
Matemàtiques
Projecció cilíndrica obliqua d’un cos sobre el pla de projecció (pla del quadre).
En aquest cas el pla del quadre és el mateix pla coordenat OXZ, i per això les rectes paralleles als eixos OZ i OX es projecten en llur veritable magnitud L’eix Y és projectat en el quadre amb una direcció dependent de la que tinguin les projectants, i sofreix, per tant, la reducció Per a les representacions en aquest sistema, caldrà conèixer la reducció de l’eix Y i el valor de l’angle XOY o YOZ, que oscillarà entre 0º i 360º aquesta relació serà constant per a totes les línies paralleles a l’eix Y L’angle que forma l’eix Y amb l’eix X podria ésser elegit indistintament, però…
perspectiva axonomètrica
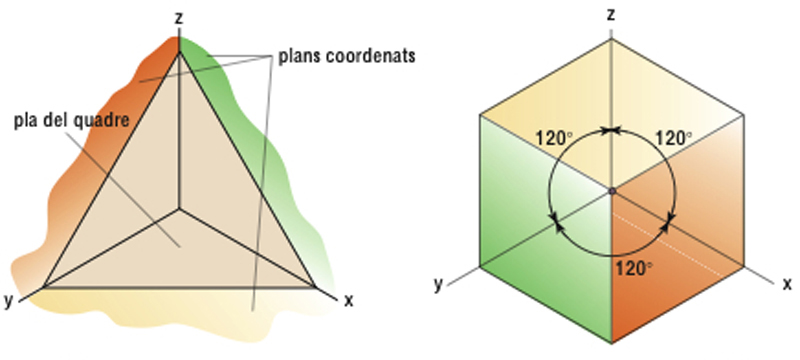
Elements de la perspectiva axonomètrica (isomètrica) i representació d’un cub
© Fototeca.cat
Art
Disseny i arts gràfiques
Matemàtiques
Sistema de representació que consisteix a referir els objectes que han d’ésser representats —mitjançant projeccions ortogonals— als plans d’un tríedre trirectangle ( plans coordenats
) i projectar-los, després, sobre un quart pla ( pla del quadre
) oblic als anteriors ( axonometria
).
El seu traçat es redueix a dibuixar les direccions dels cossos parallelament a la projecció dels eixos coordenats, relacionant amb ells les mesures d’alçada, amplada i profunditat Definit el pla del quadre, les projeccions de les arestes del tríedre sobre el pla no són donades en llurs veritables magnituds, sinó que tindran una magnitud menor Això equival a dir que totes les línies de l’espai paralleles a un pla del tríedre es veuran reduïdes en la mateixa proporció La relació entre la magnitud sobre el pla del quadre d’una de les arestes i la seva veritable magnitud és…
interval de confiança
Matemàtiques
Donat un paràmetre p a estimar, interval [p1, p2] tal que la probabilitat que el valor veritable de p hi pertanyi és igual a un valor prefixat 1-α.
Els valors p 1 i p 2 són els límits de confiança i 1-α és el nivell o grau de confiança de l’estimació L’estimació és tant més bona com més petit és l’interval de confiança i més gran el grau de confiança
teoria de la decisió estadística
Matemàtiques
Teoria matemàtica consistent en una aproximació unificadora a l’estadística matemàtica, basada en el concepte de joc d’estratègia, introduït per John von Neumann el 1928, que inclou l’estimació puntual i per intervals, com també la teoria dels contrasts d’hipòtesis.
La inicià el treball d’Abraham Wald Statistical Decisions Functions 1949 En la teoria de la decisió hom empra mostres aleatòries per tal de prendre decisions enfront d’incerteses respecte a diverses accions, entre les quals n'hi ha que poden ésser considerades millors que les restants Per exemple, en el cas d’un contrast paramètric d’hipòtesis, hom farà servir una mostra del collectiu, n'observarà una realització i, en vista de la valor presa per la funció de decisió, acceptarà o rebutjarà la hipòtesi En la teoria de la decisió, doncs, hom considera d’una banda un sistema probabilitzat o…