Resultats de la cerca
Es mostren 234 resultats
y
Matemàtiques
Símbol emprat per a designar la segona incògnita d’un sistema d’equacions.
Y
Matemàtiques
Lletra que designa l’eix vertical d’un sistema cartesià de referència en el pla coordenada).
Real Academia de Ciencias Exactas, Físicas y Naturales
Matemàtiques
Institució científica resident a Madrid que té per objecte promoure l’estudi i el progrés de les ciències.
Té el seu origen en l’Academia Naturae Curiosorum 1657 de Madrid, que fou substituïda el 1834 per l' Academia de Ciencias Naturales El seu nom actual data del 1847, i els seus estatuts, del 1921 Consta de 37 membres numeraris, de 42 corresponents i de 78 d’estrangers A més de les Memorias i dels Anales , publica la Revista de los progresos de las ciencias
Diccionario geográfico, estadístico e histórico de España y sus posesiones de ultramar
Matemàtiques
Obra de Pascual Madoz publicada a Madrid (1845-50) en 16 volums.
Conté moltes dades importants d’Espanya i de les seves característiques geogràfiques, aspectes socials i demogràfics i l’activitat econòmica preponderant Madoz tingué corresponsals arreu que li proporcionaren les dades dels pobles respectius N'han estat fetes diverses edicions facsímils parcials, entre elles la realitzada l’any 1982 per la Institució Alfons el Magnànim de València, que en publicà els articles referents a l’àmbit del País Valencià, i la feta l’any 1985 per Curial Edicions Catalanes, amb els articles referents a l’àmbit de Catalunya
Agustí Bru Zaragoza i Ebri
Arquitectura
Matemàtiques
Cristianisme
Arquitecte, eclesiàstic i matemàtic.
Estudià a València arts i teologia És autor d’un tractat d’arquitectura molt difós i utilitzat, Escuela de arquitectura civil , publicat a València el 1738, que signà amb un anagrama del seu nom en forma castellana, Athanasio Genaro Brizguz y Bru L’obra recollí la informació dels tractadistes hispànics del segle XVII, però el to i les làmines procedeixen de llibres francesos Contribuí a la difusió del gust rococó francès a València, juntament amb la tasca de Conrad Rudolf a la portada de la seu
mètode dels mínims quadrats
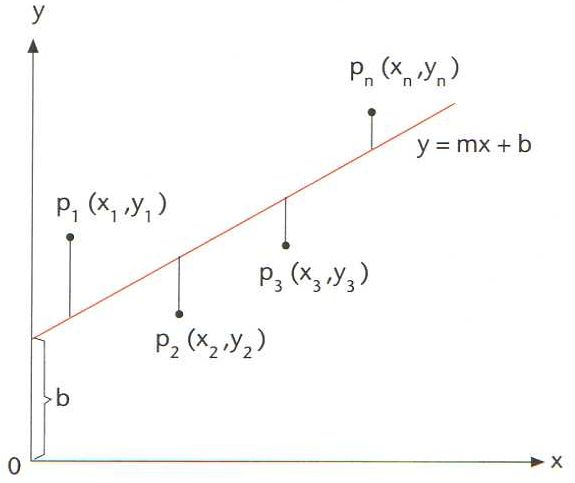
Representació de la recta y=mx + b obtinguda pel mètode dels mínims quadrats
© Fototeca.cat
Matemàtiques
Donat un conjunt de n punts del pla (x1, y1), (x2, y2), ... (xn, yn), mètode que permet de trobar l’equació y = mx + b de la recta que compleix la condició d’ésser la que més s’apropa als punts donats.
Hom defineix matemàticament la dita condició exigint que la suma dels quadrats de les desviacions, ha d’ésser mínima, entenent per desviació en un punt x i , y i la diferència d i = y i - mx i + b Hom pot demostrar que aquella condició condueix a les dues equacions a partir de les quals hom pot calcular els coeficients m i b de la recta, la qual és anomenada també recta de regressió D’altra banda, el mètode dels mínims quadrats serveix també per a ajustar funcions més complexes que la d’una recta, tals com funcions polinòmiques, exponencials, etc, i és utilitzat…
pla tangent
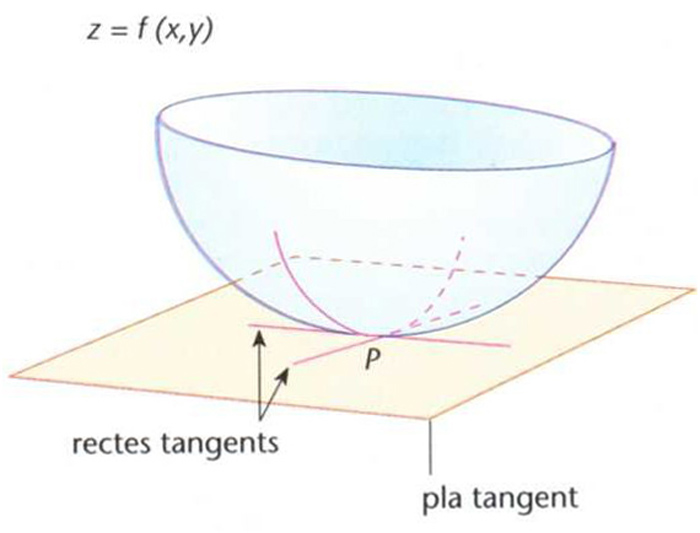
Pla tangent i dues rectes tangents a la superfície z= f(x,y) en el punt P
© Fototeca.cat
Matemàtiques
Donada una superfície z=f(x,y) i un punt P [x0, y0f(x0, y0)], pla que conté les rectes tangents en aquest punt a totes les corbes contingudes en la superfície considerada i que passen pel punt [x0, y0, f(x0, y0)].
L’equació d’aquest pla és
funció decreixent
Matemàtiques
Funció f(x) tal que x≤y⇒f(x)≥f(y).
És estrictament decreixent si x < y ⇒ f x > f y
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina