Resultats de la cerca
Es mostren 43 resultats
transformada ràpida de Fourier
Electrònica i informàtica
Tècnica per a calcular les transformades de Fourier (anàlisi de Fourier) que redueix força el nombre d’operacions i, per tant, el temps de càlcul.
En fan ús pràcticament tots els sistemes que operen amb espectres de senyals mostrejats, com ara els analitzadors de vibracions, els d’espectres o els filtres digitals ràpids
anàlisi de Fourier
Física
Matemàtiques
Estudi de les funcions que té per finalitat d’expressar-les mitjançant una sèrie o una integral en què intervenen les funcions trigonomètriques.
El fonament d’aquesta tècnica matemàtica és l’anomenat, de vegades, teorema de Fourier Tota funció periòdica f x , contínua o, com a màxim, amb un nombre finit de discontinuïtats finites, pot expressar-se mitjançant una sèrie trigonomètrica, de la següent manera la sèrie que apareix en aquesta expressió és la sèrie de Fourier de o associada a la funció f x El nombre ω és la pulsació fonamental de la sèrie de Fourier de f i és igual a la pulsació o freqüència angular de f , és a dir, ω=2π/ T , on T és el període de f El primer terme de la sèrie de…
convolució
Matemàtiques
Donades dues funcions reals de variable real, f(x) i g(x), funció definida per la integral: .
La convolució, o producte de convolució , té les propietats commutativa, associativa i distributiva Hi ha dos teoremes importants sobre la convolució El primer, o teorema de Parseval , afirma que la transformada de Laplace o de Fourier de la convolució de dues funcions és el producte de les transformades de Laplace o Fourier, respectivament, de les dues funcions F f*g y = Ff y x Fg y Segons el segon, la transformada de Fourier del producte de dues funcions és igual a la convolució de les seves transformades dividit per 2π F f x g y = 1/2π Ff…
desenvolupament en sèrie
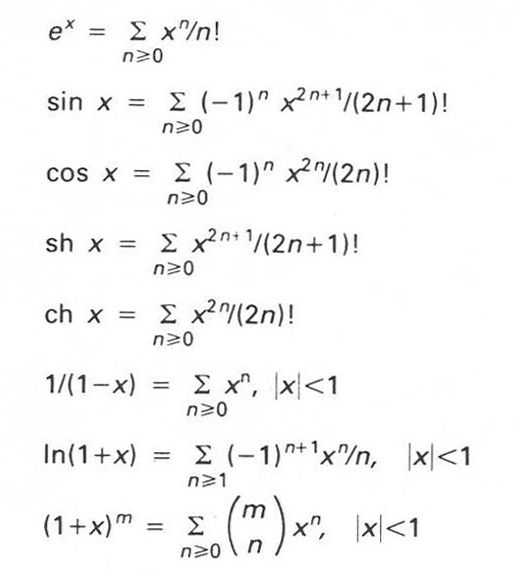
Desenvolupament en sèrie de potències d’algunes funcions
©
Matemàtiques
Expressió d’una funció real, de variable real o complexa,
f(x) ∞
, en termes d’una sèrie de funcions
:
.
La legitimitat d’aquesta igualtat depèn de la convergència de la successió de sumes parcials, en el domini de definició de fx Hom empra, generalment, el desenvolupament en sèrie de potències o sèrie entera, que resulta del teorema de Taylor , i, en el cas de funcions periòdiques, hom empra el desenvolupament en sèrie de Fourier anàlisi de Fourier
transformació integral
Matemàtiques
Operació mitjançant la qual una funció f(x) és transformada en una altra funció F(y) gràcies a relacions de tipus integral.
L’exemple més senzill és la simple integració F y = ∫ a y f x dx Una expressió vàlida per a un nombre important de transformacions integrals és F y = ∫ a b K x,y f x dx en la qual K x,y rep el nom de nucli i caracteritza l’esmentada transformació en molts casos, els límits d’integració són 0, ∞ i -∞, ∞ Cal esmentar, com a exemples importants, la integral ponderada, la integral de convolució, la transformada de Fourier anàlisi de Fourier, la de Laplace, la de Kankel, i la de Mellin
harmònic
Física
Matemàtiques
Cadascun dels termes de la sèrie de Fourier d’una funció periòdica (anàlisi de Fourier).
El terme de la sèrie de freqüència més baixa és anomenat harmònic fonamental o primer harmònic , i els altres termes són anomenats harmònics del fonamental
falansterià | falansteriana
Adepte de les doctrines de Fourier.
teorema de Riesz-Fischer
Matemàtiques
Teorema segons el qual l’espai ℒ2 de funcions de quadrat integrable respecte a una mesura m (f:Ω →ℂ, ∫|f|2dm< ∞) és un espai complet.
És un resultat bàsic en l’anàlisi de Fourier
transformada
Física
Matemàtiques
Dit d’una funció matemàtica definida mitjançant una operació en què intervé la funció que hom vol transformar, la qual cosa facilita la resolució numèrica de determinades aplicacions pràctiques.
En són exemples la transformada de Fourier, la transformada de Laplace i la transformada de Carson transformació
senyal
Tecnologia
Electrònica i informàtica
Model matemàtic de les variables d’un sistema.
Generalment, admet una descripció temporal , variacions del senyal en el temps, i una descripció freqüencial espectre , components del senyal de diversa freqüència Un senyal determinista és el que té una descripció com a funció de la variable temps x t, mentre que els senyals aleatoris solament poden ésser descrits per un model probabilístic soroll en un sistema de transmissió Els senyals analògics són definits per a tot valor de t , en contraposició als discrets en el temps o seqüències que solament ho són per a t=nT , on n és un nombre natural i T un valor determinat de t Un senyal…