Resultats de la cerca
Es mostren 6 resultats
cicloide
Cicloide
©
Matemàtiques
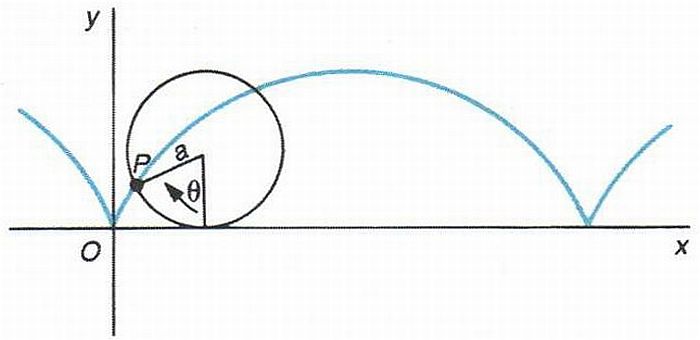
Corba engendrada per un punt fix en una circumferència que rodola, sense lliscar, damunt una recta.
Les seves equacions paramètriques són x = a θ - sinθ, y = a 1 - cosθ Hom pot ampliar aquesta definició considerant una trajectòria fixa en lloc d’una recta així, per exemple, l' epicicloide és la corba engendrada per un punt fix en una circumferència que rodola, sense lliscar, damunt una altra circumferència i exteriorment a ella
ruleta
Matemàtiques
Trajectòria descrita per un punt d’una corba, anomenada rodolant, que rodola sobre una altra anomenada base (rodolament).
Els exemples més coneguts són els de les corbes anomenades cicloide, epicicloide i hipocicloide
braquistòcrona
Braquistròcrona
© fototeca.cat
Física
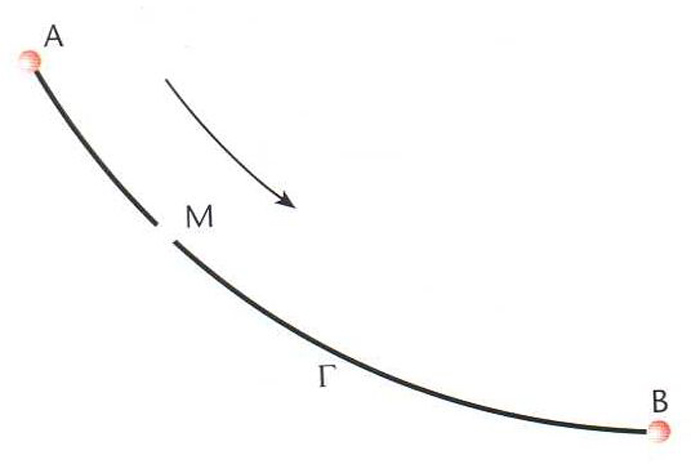
Corba que ha de recórrer una partícula que parteix del repòs i es mou per l’acció del pes i sense fregament, per tal d’unir dos punts fixs A
i B
en el mínim de temps possible.
La solució de l’eqüació diferencial que explicita analíticament el problema és una cicloide El problema de trobar aquesta corba és famós en la història de la matemàtica, car conduí Johann Bernoulli a l’establiment formal del càlcul de variacions variació
serrandell
Ictiologia
Peix de l’ordre dels pleuronectiformes, de la família dels bòtids, de 10 a 20 cm de llargada, amb els ulls sobre el costat esquerre i molt propers (la distància entre ells és menor que llur diàmetre).
Són de color grisenc amb taques més fosques i el costat dret més blanquinós, amb escates de tipus ctenoide al costat pigmentat i cicloide a l’altre L’aleta dorsal va des del nas fins al peduncle caudal, la cua és arrodonida i l’aleta anal és semblant a la dorsal i allunyada de les abdominals És un peix marí, sedentari dels fons sorrencs i llotosos de llocs poc profunds, carnívor i comestible És molt comú en certes parts del litoral dels Països Catalans, on hom el pesca sobretot a l’hivern
trocoide
Trociode
© fototeca.cat
Matemàtiques
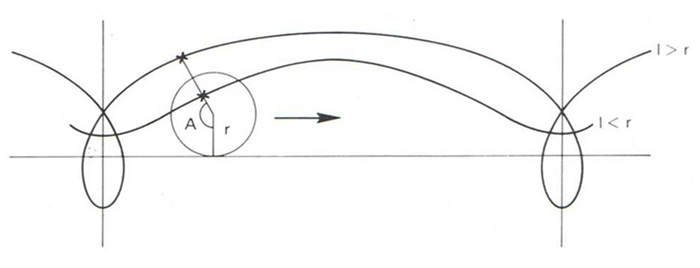
Corba descrita per un punt fixat a un cercle quan aquest cercle roda sense lliscament sobre una línia recta fixa.
Si el radi del cercle és r , la distància del punt generador al centre del cercle és l i A és l’angle determinat pel punt quan el cercle ha rodat A radiants, aleshores les equacions paramètriques de la trocoide són x = rA-l sin A y = r-l cos A Si l és major que r punt exterior al cercle, la trocoide descriu rulls si l és menor que r punt interior al cercle, la trocoide no toca mai la línia recta fixa base del desplaçament si el punt és el centre del cercle, la trocoide és una recta si l és igual a r punt de la circumferència, la trocoide és aleshores una cicloide
epicicloide
Epiciloide
© fototeca.cat
Matemàtiques
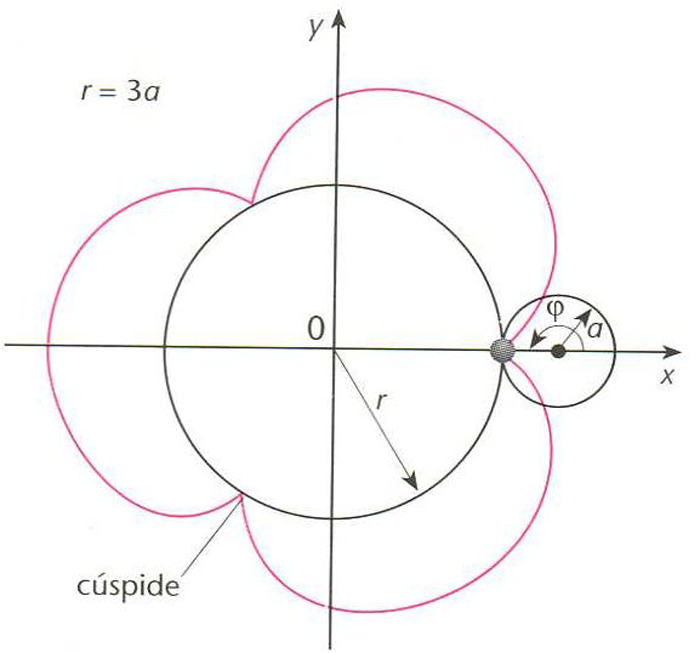
Corba descrita per un punt d’una circumferència que roda sense lliscar sobre una altra, mantenint-se tangents exteriorment ( cicloide
).
La seva equació és on r és el radi de la circumferència fixa, i a , el radi de la circumferència mòbil Si r = na , l’epicidoide té n cúspides n , nombre natural Si r = a la corba degenera en una cardioide Si r= 2 a , ho fa en una nefroide