Resultats de la cerca
Es mostren 55 resultats
Claude Delvincourt
Música
Compositor francès.
Compaginà els estudis de dret amb els de música al Conservatori de París, on fou alumne de L Boëllmann, H Büsser i G Caussade El 1913 guanyà el Premi de Roma de composició amb la cantata Faust et Hélène Durant l’època en què estigué al capdavant del Conservatori de Versalles 1931-41 en dirigí la reforma pedagògica, i durant l’ocupació nazi fundà l’Orchestre des Cadets i un cor infantil per tal d’impedir la deportació dels alumnes a Alemanya El control cartesià que marcà la seva música no impedí, però, l’expressió dels sentiments, i les seves composicions revelen un esperit…
ontologisme
Filosofia
Doctrina segons la qual l’ésser, les idees eternes i universals, constitueixen l’objecte immediat i directe de la ment i només mitjançant la comprensió quasi-intuïtiva d’aquest objecte poden ésser copsats intel·lectualment els altres objectes del coneixement (hom veu totes les coses en l’ésser).
Bé que l’ontologisme sorgeix al s XIX com a reacció a l’idealisme i en oposició al psicologisme de tipus cartesià, no és just d’identificar-lo amb el realisme ni és sovint aliè a una certa tendència psicologista això darrer, per exemple, és el que critica VGioberti en l’actitud d’ARosmini-Serbati relativa al coneixement de Déu per l’home La primacia de l’ontològic sobre el gnoseològic i epistemològic pot certament trobar en Plató, sant Agustí, sant Anselm i altres uns destacats antecessors tanmateix, pròpiament hom pot parlar d’ontologisme només en relació amb NMalebranche i…
nombre complex
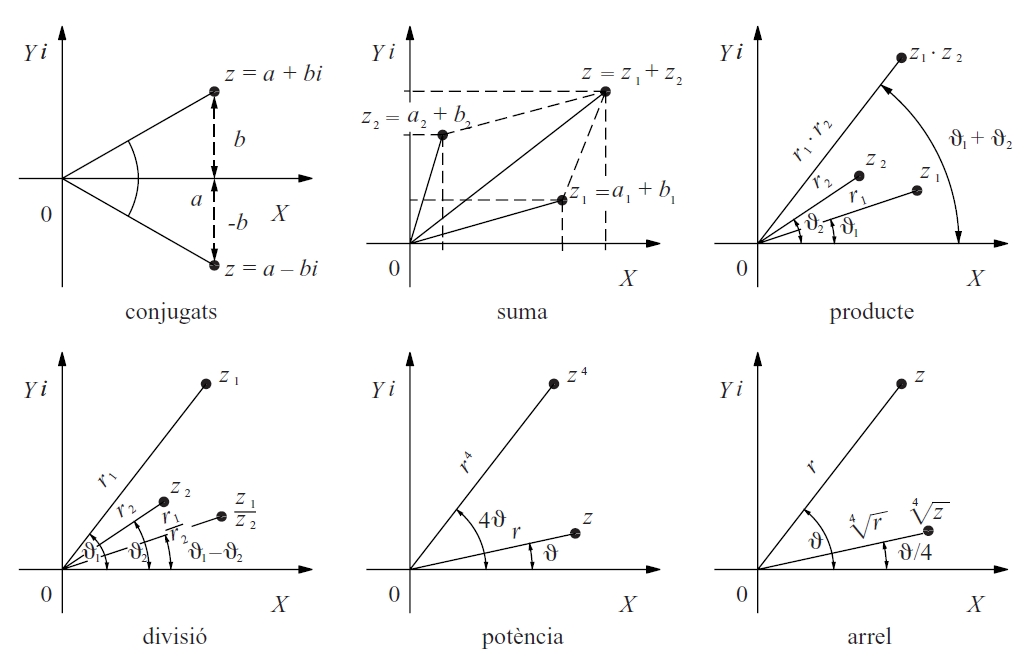
Nombres complexos
Matemàtiques
Nombre que pot ésser expressat com a suma d’un nombre real i d’un nombre imaginari.
Hom construeix el conjunt ℂ dels nombres complexos afegint al conjunt dels nombres reals un nombre nou, no real, que hom representa per una i , i que és definit formalment per la propietat que el seu quadrat és -1 Hom estén a aquest conjunt ℂ les operacions d’addició i de multiplicació amb totes les propietats que tenen entre nombres reals Cada nombre complex pot ésser escrit en forma de polinomi de primer grau en i , a + bi , i pot ésser representat geomètricament en el pla prenent a i b com a coordenades en un sistema cartesià ortogonal pla d'Argand-Gauss Aquesta…
monisme
Filosofia
Doctrina segons la qual només hi ha una substància, respecte a la qual tota altra substància és negada o és simplement reduïda a manifestació de l’altra.
Fonamentalment reduccionista, el monisme pot ésser dividit en dos tipus el místic i el panteista Representant típic del primer és Plotí, el concepte de l’U del qual és el principi que dóna lloc a l’oposició de subjecte i objecte mitjançant el procés d’emanacions Quant al segon tipus, n'és representant Spinoza, que resol el dualisme cartesià cos-ànima, així com els dualismes d’esperit pensament i matèria extensió i de Déu i món Parmènides, entre els antics, i Schelling, en la modernitat, poden també ésser adjuntats al monisme, però només molt impròpiament poden ésser-ho els…
cartesianisme
Filosofia
Conjunt de doctrines de Descartes (llatinitzat Cartesius
), i també corrent ideològic derivat d’ell, que influí en tot el pensament europeu dels s. XVII i XVIII.
A França es difongué, malgrat el decret del Sant Ofici 1663 i la prohibició reial d’ensenyar-lo 1671, gràcies a la fervent adhesió del pare Mersenne, dels oratorians Bérulle i Malebranche, del nucli de Port-Royal, i de Cordemoy, La Fargue i Régis Trobà una forta oposició en els peripatètics, els atomistes i els empiristes, i també la generalitzada dels jesuïtes, pedagogs de l’època El cartesianisme augustinià de Malebranche és la més vigorosa de les branques indicades Obtingué un èxit semblant als Països Baixos Guellinx, Spinoza, però no tant a Alemanya Clauberg ni a Anglaterra, indrets d’on…
Ruggero Giuseppe Boscovich
Astronomia
Física
Matemàtiques
Físic, astrònom i matemàtic italià, d’origen croat.
Cursà estudis de física i matemàtiques al Collegium Romanum, i el 1726 entrà a la Companyia de Jesús En collaboració amb Christopher Mainer amidà l’arc de meridià entre Roma i Rímini 1750-53 En ésser els jesuïtes expulsats d’Itàlia el 1773, anà a París per invitació de Lluís XIV, on li fou concedida la direcció del departament d’òptica naval fins el 1782, que tornà a Itàlia A la seva obra fonamental, Theoria philosophiae naturalis redacta ad unicam legem virium in natura existentium Viena, 1758, criticà els conceptes fonamentals de l’obra de Newton, considerant-los similars als suscitats per…
uniformitat
Matemàtiques
Família F de subconjunts d’un producte cartesià T × T
.
Compleix x,x pertany a qualsevol element de F , per a tot x si V és de F, V - 1 = { x,y | y,x és de V} és també de F i per a tot V de F existeix un altre W tal que WW = { x,z | existeix y en T i x,y ∈ W , y,z ∈ W} és un subconjunt de V Tota uniformitat dóna lloc a un espai topològic i aquest és metritzable la seva topologia prové d’una distància si és de Hausdorff i la uniformitat té una base numerable Per exemple, si T és un espai mètric, amb distància d , el conjunt de subconjunts de T × T , U ∈ = { x,y | d x,y πε} és una uniformitat La parella T,F , on T és conjunt i F…
parella
Matemàtiques
Cadascun dels elements d’un producte cartesià de dos conjunts.
triplet
Matemàtiques
Cadascun dels elements d’un producte cartesià de tres conjunts.
símbol
Matemàtiques
Lletra o signe gràfic de qualsevol mena utilitzat per a representar quantitats (nombres), relacions o operacions.
Cal distingir sempre el símbol del concepte Així, el nombre dos concepte pot ésser representat per símbols diferents 2, II, ╫, etc Principals símbols símbols emprats en teoria de conjunts ∈ pertany a ∉ no pertany a = igual a ≠ diferent ⊂ inclusió, és inclòs en ⊄ no és inclòs en ⋂ intersecció ⋃ reunió − diferència ∁ , − , ∽ complementari ∆ diferència simètrica → aplicació, funció ≃ coordinable, bijectiu x producte cartesià {} singletons claudàtors ∅ conjunt buit ℕ nombres naturals ℤ nombres enters ℚ nombres racionals ℝ nombres reals ℂ nombres complexos símbols…