Resultats de la cerca
Es mostren 26 resultats
Roger Penrose
Física
Matemàtic i físic anglès.
Llicenciat en matemàtiques i doctorat a Cambridge 1958, és membre de la Royal Society des de l’any 1972 Catedràtic de matemàtiques a la Universitat d’Oxford 1973-99, càtedra de la qual restà professor emèrit El 1955 publicà un estudi per a l’aplicació de la inversa generalitzada en la resolució matrius d’equacions lineals Feu popular la representació d’un triangle format per tres trams rectes de secció quadrada, units formant un angle recte en cadascun dels extrems i d’altres figures que no poden existir en un espai euclidià ordinari, anomenades des de llavors figures de Penrose…
coordenades cartesianes
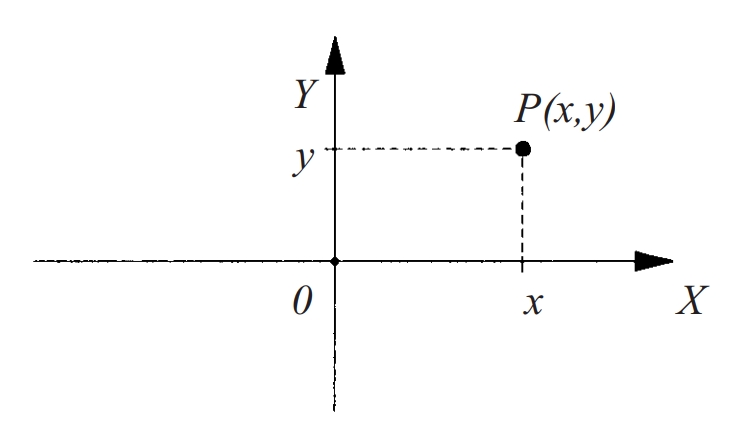
coordenades cartesianes al pla
Matemàtiques
En un espai euclidià, coordenades afins respecte d’una referència afí.
En el cas d’una referència, es diu que les coordenades són cartesianes rectangulars Així, tot punt del pla espai P s’identifica amb les seves coordenades x , y x , y , z on cada coordenada representa la projecció de P en l’eix corresponent d’acord amb la direcció dels altres eixos També s’usen referències no ortogonals coordenades cartesianes a l’espai
pla

Equació del pla
© fototeca.cat
Matemàtiques
Superfície tal que qualsevol recta que passi per dos dels seus punts es troba totalment continguda en la dita superfície.
Els plans, juntament amb els punts i les rectes, són els elements geomètrics primitius en l’axiomatització de Hilbert de la geometria D’altra banda, un pla és determinat per tres punts no alineats, o bé per dues rectes que es tallin o siguin paralleles, o bé per un punt i una recta que no contingui el punt A l’espai euclidià ℝ 3 un pla pot ésser representat per l’equació A x— x 1 + B y— y 1 + C z— z 1 = 0, en la qual x 1 , y 1 , z 1 són les tres coordenades d’un punt P 1 donat del pla, A, B, C són les tres components d’un vector N normal al pla, i x, y, z són les tres…
grup
Matemàtiques
Estructura algèbrica constituïda per un conjunt G on hi ha definida una operació, designada per *, que per a qualssevol elements a, b, c de G té aquestes tres propietats: propietat associativa, o sia (a*b) *C = a*(b*c); G conté un element neutre e, o sia a*e = a; i per a qualsevol element a n’hi ha un altre de G, representat per a’, que és el seu invers (a*a’ = a’*a = e).
Si a més es compleix la propietat commutativa a*b = b*a , el grup és anomenat commutatiu o abelià i, en aquest cas, si hom representa l’operació amb el signe +, el grup és anomenat també additiu , mentre que si hom utilitza el signe o uns altres, el grup és anomenat també multiplicatiu Hom anomena ordre d’un grup el nombre d’elements que conté més exactament, és el cardinal del conjunt dels seus elements El grup és anomenat cíclic si qualsevol element s’obté per producte repetit d’un de fix, anomenat generador L’estudi en abstracte dels grups permet d’obtenir resultats aplicables a grups…
figures de Penrose
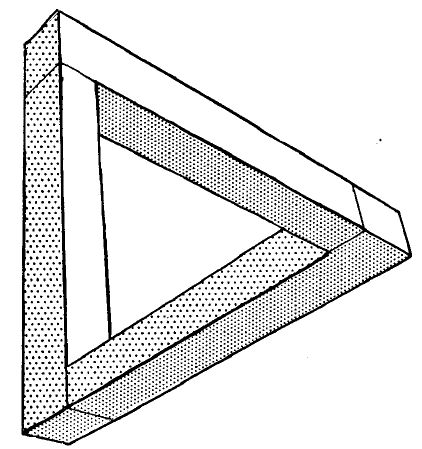
Triangle de Penrose
Representacions bidimensionals de figures tridimensionals que no poden existir en un espai euclidià ordinari.
El físic i matemàtic Roger Penrose féu popular la representació d’un triangle format per tres trams rectes de secció quadrada units formant un angle recte en cadascun dels extrems
base ortonormal
Matemàtiques
Base d’un espai vectorial euclidià formada per vectors que són ortogonals dos a dos.
Per exemple, a ℝ n la base canònica és ortonormal respecte al producte escalar
transformació simètrica
Matemàtiques
Transformació T d’un espai euclidià E tal que Tx·y = x·Ty si · indica el producte escalar de E.
teorema de Bolzano-Weierstrass
Matemàtiques
Teorema segons el qual tot conjunt infinit i afitat d’un espai euclidià té almenys un punt d’acumulació i tota successió infinita afitada té almenys un punt límit
espai vectorial
Matemàtiques
Grup abelià E
en el qual hi ha definida una llei de composició externa amb elements d’un cos K
, K
× E
→ E tal, que al parell (λ, e
) correspon l’element λ e
.
I acomplint-se les propietats λ + μ e = λ e + μ e , λ e + f = λ e + λ f , λμ e = λμ e i 1 e = e Els elements de E són anomenats vectors , i els elements de K , escalars Una part de E que sigui subgrup respecte a la suma i que sigui estable respecte al producte per qualsevol escalar, és anomenada subespai de E , i amb les mateixes operacions de E és un altre espai vectorial Si F és un subespai de E , hom pot definir congruències a E mitjançant la relació d’equivalència x ≡ y mòd F , si i només si la diferència x — y pertany a F Això permet de formar el conjunt quocient E/F quocient, el…
lepidòpters

Papallona rei (Papilio machaon)
Duarte Frade iNaturalist (cc-by-nc-4.0)
Entomologia
Ordre d’insectes de la subclasse dels pterigots que es caracteritzen pel fet d’atènyer de 0,2 a 30 cm.
Hom utilitza sovint les denominacions macrolepidòpter i microlepidòpter per a designar respectivament les papallones grosses de 2-3 cm o més i les papallones petites de 2-3 cm o menys Tenen les quatre ales i la major part del cos cobertes d’escates, sovint molt acolorides El cap, petit, conté nombrosos òrgans els ulls composts, els palps, les antenes amb què els mascles capten les feromones de les femelles i l’espiritrompa, amb la qual xuclen el nèctar i d’altres sucs vegetals i, en fer-ho, traslladen el pollen, adherit al seu cos, d’una flor a una altra pollinització creuada La fase larval…