Resultats de la cerca
Es mostren 32 resultats
reflexió

Trajectòria dels raigs en la reflexió
© Fototeca.cat
Física
Modificació de la trajectòria d’una partícula, d’un raig o del front d’una ona quan incideixen sobre una superfície límit del medi per on es mouen.
En el cas particular dels raigs, hom pot provar que la recta normal de la superfície reflectora, el raig incident i el reflectit són coplanaris, formant l’anomenat pla de reflexió , alhora que els angles formats per cadascun dels raigs amb la normal anomenats angle d’incidència î i angle de reflexió r són iguals Quan una ona és parcialment reflectida en una superfície, hom defineix el coeficient de reflexió R com R = I r / I i , on I i és la intensitat de l’ona incident i I r és la de l’ona reflectida En el cas particular de la reflexió d’una partícula per una superfície també es compleixen…
mòdul de rigidesa
Física
Tecnologia
Quocient entre un esforç tallant o de cisallament, expressat en kg/cm2, i la deformació angular que produeix, expressada en radiants.
És anomenat també mòdul d’elasticitat en cisallament , i es relaciona amb el mòdul de Young mitjançant la fórmula G = E /1 + μ 2 , on μ designa el coeficient de Poisson
excés esfèric
Matemàtiques
En un triangle esfèric, d’angles A, B i C mesurats en radiants, quantitat donada per la fórmula E = A+B+C-π.
en oposició
Electrònica i informàtica
Física
Dit de dues magnituds periòdiques d’igual període que presenten una diferència de fase entre elles de mig període, o sia π radiants.
funció sinus
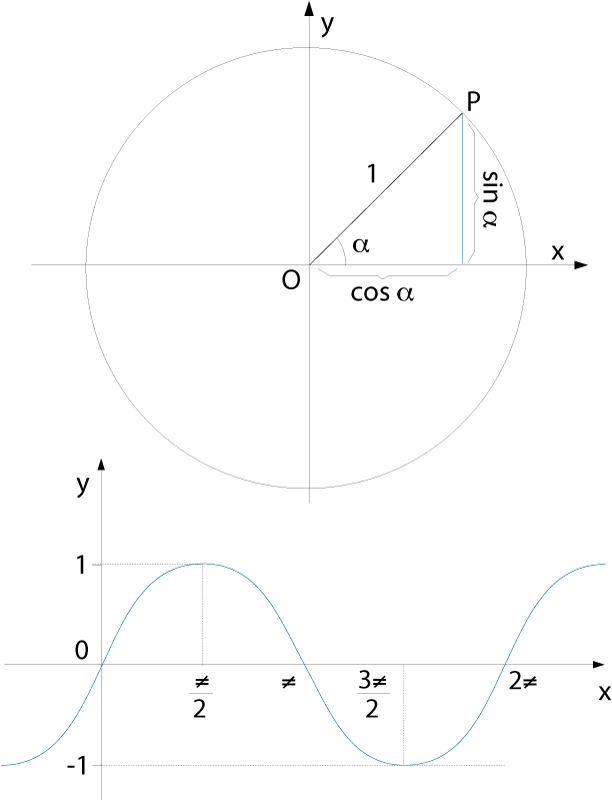
Representació gràfica del sinus d’un angle (a dalt) i de la funció sinus (a baix)
© Fototeca.cat
Matemàtiques
Funció sin: ℝ→ℝdefinida per l’assignació x →sin (x) on sin(x) és el sinus de l’angle que fa x radiants.
És una funció periòdica de període 2π i el seu recorregut és l’interval -1,1 És una de les sis funcions trigonomètriques o circulars i està relacionada amb la funció cosinus per la derivada d sin x / dx =cos x , d cos x / dx = -sin x És indefinidament derivable i el seu desenvolupament en sèrie entera és En termes de la funció exponencial complexa té l’expressió sin x= e i x - e i x /2 i , relació que permet d’estendre-la al cos dels nombres complexos, resultant-ne la funció sinus complex
funció cosinus
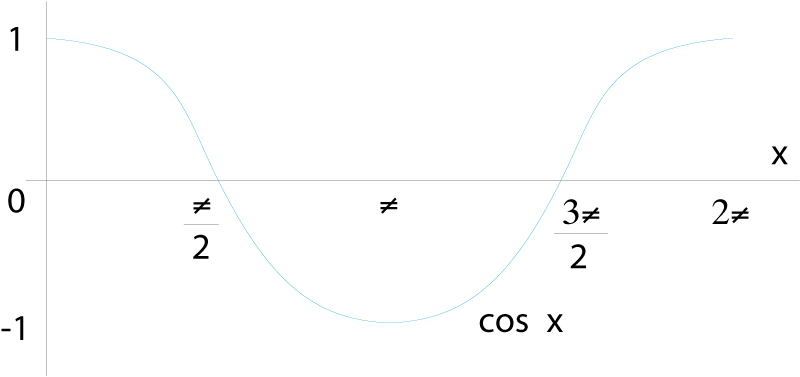
Representació gràfica de la funció y=cos x
© Fototeca.cat
Matemàtiques
Funció cos: ℝ→ℝdefinida per l’assignació x →cos (x), on cos(x) és el cosinus de l’angle que fa x radiants.
És una funció periòdica de període 2π i el seu recorregut és l’interval -1, 1 És una de les sis funcions trigonomètriques o circulars i està relacionada amb la funció sinus per la derivada dcos x/ dx = -sin x, dsin x/ dx = cos x És indefinidament derivable, i el seu desenvolupament en sèrie entera és En termes de la funció exponencial complexa té l’expressió cos x=e i x + e - i x /2, relació que permet d’estendre-la al cos dels nombres complexos, resultant-ne la funció cosinus complex
puntual
Astronomia
Física
Dit de les fonts radiants les dimensions de les quals poden ésser negligides i, per tant, poden ésser considerades matemàticament com un punt emissor.
en quadratura
Electrònica i informàtica
Física
Dit de dues magnituds periòdiques d’igual període que presenten una diferència de fase entre elles d’un quart de període, o sia π/2 radiants.
funció tangent
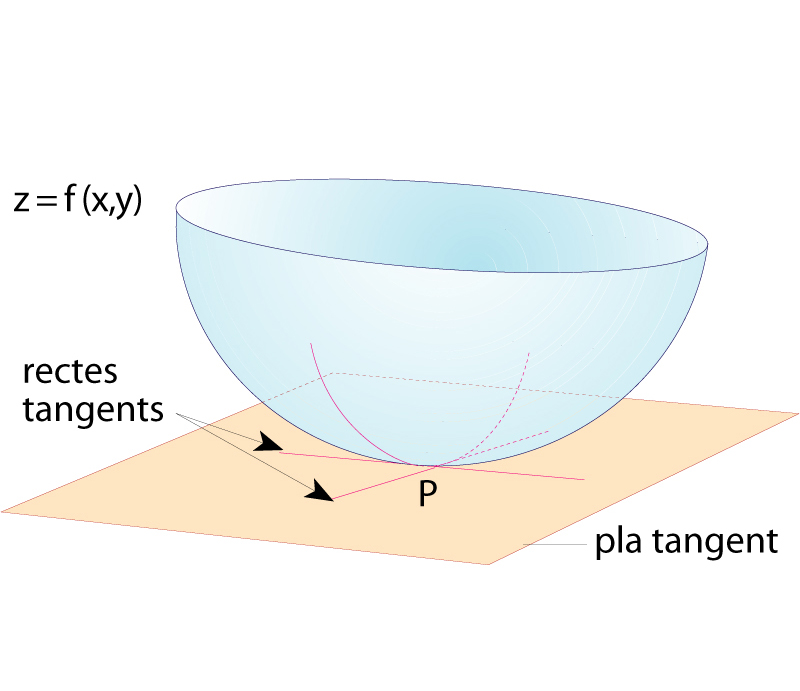
Pla tangent i dues rectes tangents a la superfície z=f(x,y) en el punt P
© Fototeca.cat
Matemàtiques
Funció tg: →-{π/2+kπ, k ∈ℤ} →ℝ, definida per l’assignació x
→tg x
, on tg x
és la tangent de l’angle que fa x
radiants.
És una funció periòdica de període 2 i el seu recorregut és -∞, ∞ És una de les sis funcions trigonomètriques o circulars i està relacionada amb les funcions sinus i cosinus per l’expressió tg x =sin x /cos x És indefinidament derivable i el seu desenvolupament en sèrie entera és quan x 2
trigonometria

1, circumferència de referència per a la definició de les raons trigonomètriques; 2, representació gràfica de les línies trigonomètriques; 3, símbols emprats en la resuloció de triangles
© fototeca.cat
Matemàtiques
Part de la matemàtica inicialment dedicada a l’estudi de les relacions entre les amplituds dels angles i les longituds dels segments que llurs costats determinen en les rectes que tallen.
La trigonometria es basa en les propietats de les anomenades raons trigonomètriques , que són definides a partir d’un punt P x,y d’una circumferència de centre O i per l’angle α que forma el radi r = OP amb l’eix OX , mitjançant els sis quocients següents sin α = y/r sinus cos α = x/r cosinus tg α = y/x tangent cotg α x/y cotangent sec α = r/x secant cosec α = r/y cosecant Quan el punt P és a una distància r = 1 de l’origen O , el valor absolut d’aquestes raons és representat per la longitud de certs segments anomenats línies trigonomètriques , respectivament, fàcils de traçar A partir de…