Resultats de la cerca
Es mostren 1209 resultats
creu doble

Creu doble
© Fototeca.cat
quadrilàter
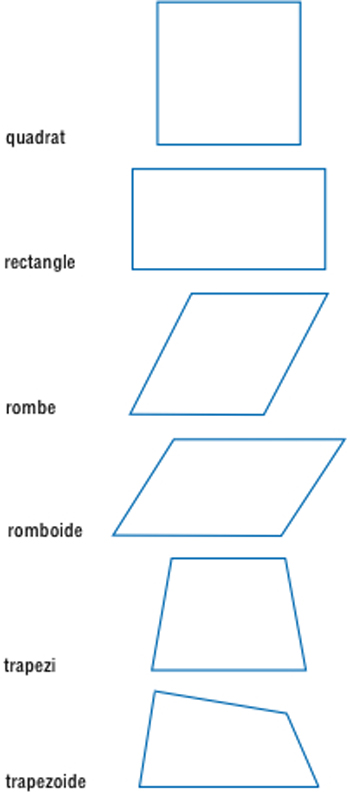
Diferents quadrilàters
© Fototeca.cat
Matemàtiques
Polígon que té quatre costats.
Un quadrilàter on els costats oposats són parallels és dit parallelogram, un parallelogram amb els quatre angles rectes és un rectangle si aquest té els quatre costats iguals és dit quadrat Un rombe és un quadrilàter amb els quatre costats iguals Un quadrilàter amb dos costats parallels és un trapezi
baldufa
Tecnologia
Qualsevol cos que gira recolzat només en un punt.
Hom distingueix la baldufa asimètrica , per a la qual els moments d’inèrcia segons l’eix de gir i segons dos eixos perpendiculars entre ells i amb l’eix de gir són diferents, la baldufa simètrica , per a la qual els dos darrers són iguals, i la baldufa esfèrica , els tres moments d’inèrcia de la qual són iguals L’estudi del moviments precessió, nutació de la baldufa simètrica ha esdevingut clàssic en mecànica giroscopi
topologia

Topologia Les figures unides amb fletxes són topològicament iguals, perquè és possilbe passar de l’una a l’altra per mitjà d’una transformació contínua
© Fototeca.cat
Matemàtiques
Part de la matemàtica que estudia aquelles propietats dels conjunts de punts de la recta, del pla, de l’espai o d’espais de dimensions superiors que no són alterades per les transformacions contínues.
Es tracta de propietats geomètriques que no depenen de cap magnitud, sinó únicament de la posició relativa dels punts Per exemple, el fet que dos punts puguin unir-se o no per un camí, o que el nombre de cares menys el d’arestes més el de vèrtexs d’un políedre esfèric sigui sempre dos teorema d’Euler Aquí hom entén per transformació contínua aquella que admet una inversa i que tant ella com la inversa són contínues L’íntima connexió que hi ha entre el concepte de continuïtat d’una funció en un punt i el d’entorn d’un punt permet de transportar l’estudi de propietats topològiques…
llei de les àrees
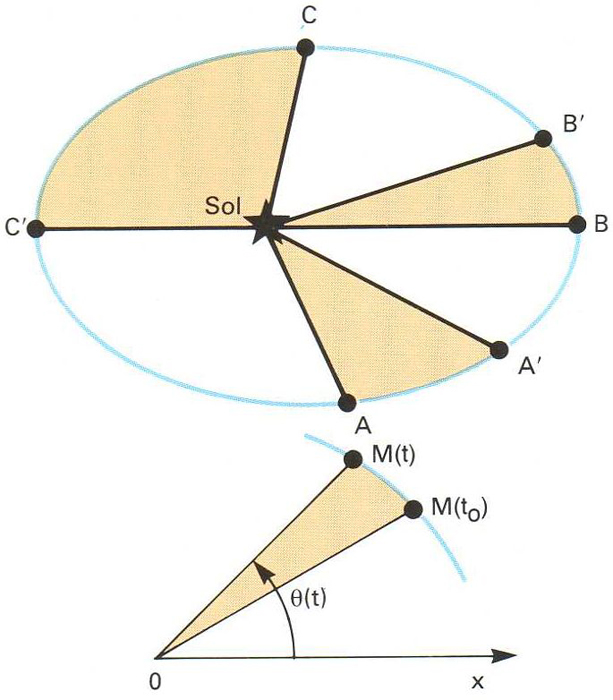
Llei de les àrees aplicada a l’òrbita d’un planeta: les àrees contingudes entre els punts AA’, BB’ i CC’ són iguals perquè es recorren en temps iguals. El radi vector escombra àrees iguals en temps iguals
© fototeca.cat
Física
Teorema referit al moviment d’un punt sotmès a un sistema de forces centrals, que demostra que les àrees descrites pels radis vectors r
©són proporcionals al temps emprat per a descriure-les.
En astronomia, aquest teorema és aplicat a l’estudi del moviment d’un planeta respecte al Sol i és conegut com la segona de les tres lleis de Kepler La demostració és obtinguda d’aplicar el teorema del moment angular al cas particular del moviment d’un punt material M sotmès a un sistema de forces centrals que passen pel punt O , respecte al qual hom obté els moments Aquests moments tenen una resultant nulla i, per tant, el moment angular L és un vector constant perpendicular sempre als radis vectors, que descriuran com a conseqüència una trajectòria plana Si hom considera la posició de M en…
lleis de Kepler
Astronomia
Lleis empíriques que descriuen el moviment dels planetes entorn del Sol.
Foren descobertes per J Kepler aprofitant les dades obtingudes per T Brahe astronomia Segons la primera llei , l’òrbita de cada planeta és una ellipse, un dels focus de la qual és ocupat pel Sol La segona llei , anomenada també llei de les àrees , estableix que el radi vector d’un planeta escombra àrees iguals en temps iguals Segons la tercera llei , el quadrat del període de revolució orbital d’un planeta és proporcional al cub del semieix major de la seva òrbita
mesura
Música
Divisió del temps musical en parts iguals.
Hom en troba els orígens en la mètrica grega, en la qual cada vers era format per peus, llargs o breus
equale
Música
Peça per a veus o instruments iguals.
Durant el segle XVIII, i especialment a Àustria, aquest terme designava més concretament les obres de caràcter solemne, escrites per a quatre trombons i destinades a ser interpretades durant un funeral Un dels exemples més coneguts són els tres equali per a quatre trombons de L van Beethoven
pindoler
Farmàcia
Aparell emprat per a fer píndoles.
El més conegut és el de Dieterich , que consta d’una peça amb canals semicilíndrics d’uns 5 mm de diàmetre, sobre la qual hom aplica una altra peça igual, subjecta a un mànec de fusta que fa córrer sobre la peça anterior per tal de tallar el magdaleó en parts iguals Hi ha pindolers de més rendiment, que són circulars com el de Swidkes Els de tipus industrial com ara el de Kilian tenien dos cilindres acanalats transversalment, que giraven en sentit contrari i tallaven els magdaleons en esfèrules iguals Actualment, els pindolers són peces de museu
polígon
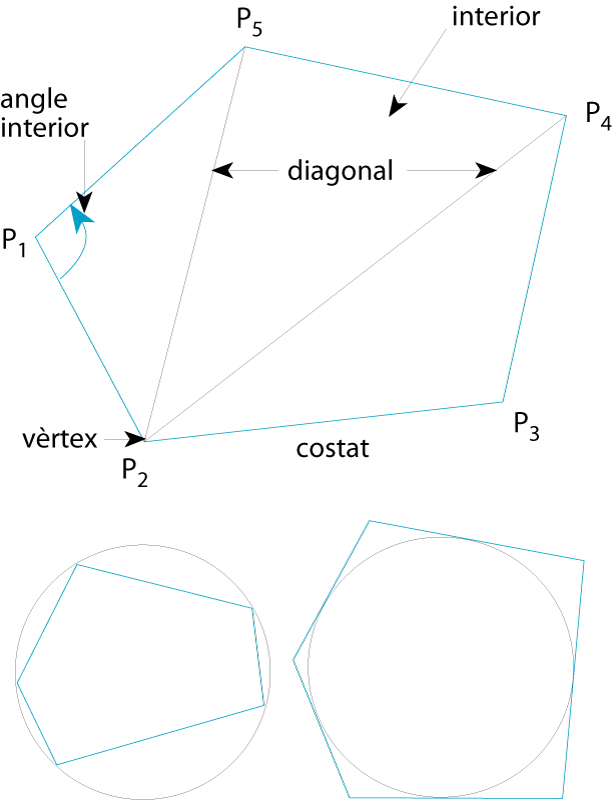
Elements d’un polígon (dalt); polígon inscrit en un cercle (baix esquerre); polígon circumscrit a un cercle (baix dreta)
© Fototeca.cat
Matemàtiques
Figura plana i tancada formada per segments rectes.
P 1 P 2 , P 2 P 3 , P n - 1 P n , i P n P 1 , són anomenats costats del polígon, essent els punts P 1 , P 2 , , P n , amb n ≥3, els anomenats vèrtexs del polígon Una diagonal del polígon és el segment recte que uneix dos vèrtexs no correlatius La porció de pla que és envoltada pels costats constitueix l' interior del polígon Els angles determinats per cada parell de costats adjacents, i que són a l’interior, són dits angles interiors del polígon Un polígon és convex si cada angle interior és menor o igual a 180° Un polígon és còncau si no és convex, és a dir, si almenys existeix un angle…