Resultats de la cerca
Es mostren 462 resultats
Àlgebra i geometria diferencial (A. Connes); equacions diferencials (S.T. Yan); topologia (W.P. Thurston)
Àlgebra i geometria diferencial A Connes equacions diferencials ST Yan topologia WP Thurston
Construcció de polígons, teoria de nombres, geometria diferencial, geometria no euclidiana, teorema fonamental d’àlgebra, astronomia, geodèsia, grans problemes (Gauss)
Construcció de polígons, teoria de nombres, geometria diferencial, geometria no euclidiana, teorema fonamental d’àlgebra, astronomia, geodèsia, grans problemes Gauss
K-teoria, teorema d’índex d’operadors el·líptics (Atiyal-Singer); topologia diferencial (S. Snade); àlgebra homològica i algebraica. K-teoria (A. Grothendieck)
K-teoria, teorema d’índex d’operadors ellíptics Atiyal-Singer topologia diferencial S Snade àlgebra homològica i algebraica K-teoria A Grothendieck
factor integrant
Matemàtiques
Funció M(x,y) que permet la integració d’una equació diferencial, per mitjà de la transformació d’aquesta en diferencial exacta.
Així, donada l’equació diferencial Ax,ydx + Bx,ydy = 0, multiplicant-la pel factor integrant Mx,y hom obté Mx,y Ax,y dx + Mx,y Bx,y dy = 0, que és diferencial exacta i, per tant, fàcilment integrable No sempre hi ha un factor integrant, i quan hi és, no és únic
tub de Pitot
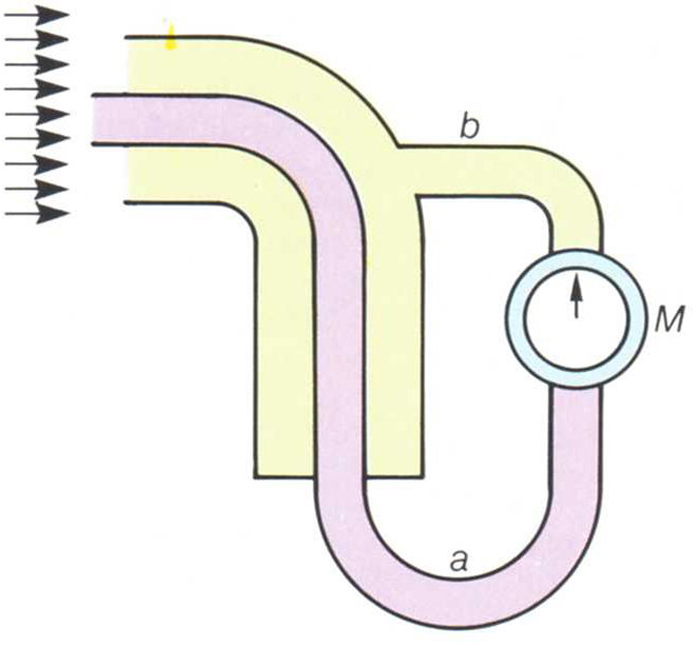
Esquema d’un tub de Pitot: el manòmetre diferencial M mesura la diferència entre la pressió dinàmica (que mesura pel tub a) i la pressió estàtica (que mesura pel tub b) del fluid, el moviment del qual és assenyalat per les fletxes
©
Física
Instrument que permet de mesurar la velocitat d’un fluid respecte a un cos immòbil o la d’un mòbil al si d’un fluid.
Consisteix en dos tubs coaxials doblegats en angle recte, de manera que un dels braços sigui parallel al corrent del fluid o a la direcció del mòbil El tub exterior, que és tancat per tots dos extrems i connectat a un manòmetre diferencial per un orifici lateral, enregistra la pressió estàtica, P e , és a dir, la pressió del medi ambient El tub interior, connectat al manòmetre per l’extrem oposat al d’entrada del fluid, enregistra la pressió dinàmica del corrent, P d , funció de la velocitat El manòmetre diferencial, en donar la diferència d’ambdues pressions, indica…
funcions de Bessel de primera classe
Matemàtiques
Solucions de l’equació diferencial de Bessel, de la forma
on Γ és la funció gamma.
J - n x n’és també una solució particular Si n és un nombre enter J - n x = -1 n J n x en canvi, si n no és enter J n x i J - n x són independents, de manera que la solució general de l’equació diferencial de Bessel és y x = aJ n x + bJ - n x ,en què a i b són constants
equació de Riccati
Matemàtiques
Equació diferencial de la forma y´ = dy/dx = f1(x) + y f2(x) + y2 f3(x).
No té una solució general calculable per quadratures, però si hom en coneix una solució particular y 0 , aleshores és fàcil de trobar-ne la solució general Fent el canvi y = y 0 + z , resulta l' equació de Bernoulli z´ = z f 2 x + 2 f 3 x y 0 + z 2 f 3 x , i fent el nou canvi u = 1/ z , hom n'obté una equació diferencial lineal d’integració immediata
estructura dels salaris
Economia
Dret del treball
Conjunt de relacions entre els diferents components de la renda salarial a nivell macroeconòmic, que es componen de les diferències de remuneració entre treballadors, anomenades salari diferencial
.
Són causes d’aquest salari diferencial les diversitats professionals o ocupacionals, el sector o empresa on es treballi, l’àrea on és situada l’empresa, el sexe, etc
carry trade
Economia
Pràctica especulativa consistent a endeutar-se en una divisa amb tipus d’interès molt baix per a comprar divises o actius amb el tipus d’interès molt més elevat, beneficiant-se així del diferencial.
El risc és major com més alt és el diferencial El carry trade és darrere de la fallida de l’estat d’Islàndia, on els bancs l’utilitzaven per a adquirir bons del país S'acostuma a practicar amb monedes d’economies emergents, que es veuen forçades a establir elevats tipus d’interès per a atreure capitals
condicions de contorn
Física
Matemàtiques
Donada una equació diferencial, condicions que cal imposar a la solució general per tal que prengui uns determinats valors en punts o zones concrets del domini de valors de la variable independent, zones anomenades contorns del problema.
Per exemple, el potencial electroestàtic d’una distribució de càrregues elèctriques ha de satisfer l’equació diferencial de Laplace ∇ 2 V =0 amb la condició de contorn que V sigui constant sobre la superfície dels conductors que hi hagi a l’espai del problema Les condicions de contorn són imposades per les lleis físiques, per la simetria o per la disposició experimental del problema Si el problema dinàmic és controlat per una o diverses equacions diferencials en derivades parcials, la solució particular del problema generalment ha de satisfer, a més d’unes condicions de contorn,…