Resultats de la cerca
Es mostren 5503 resultats
residual
Matemàtiques
Dit de cadascuna de les classes d’equivalència que resulta en el conjunt ℤquan hom considera la relació a R b ⇔b-a = m(m ∈ℤ).
relació
Matemàtiques
Lligam entre diversos elements d’un conjunt.
Per tal de precisar aquesta idea intuïtiva, hom defineix la relació com a qualsevol subconjunt d’un producte cartesià del conjunt amb ell mateix és a dir, que els elements són relacionats si formen un element del subconjunt En general, en una relació intervé un nombre determinat d’elements n així, una relació d’ordre entre els elements és un subconjunt del producte de n conjunts A El tipus de relació més freqüent és aquella en què n = 2, anomenada relació binària , que és un subconjunt de A × A Si els dos elements són a i b , hom diu que a R b , o que a és relacionat amb b —o…
translació
traslació
Tecnologia
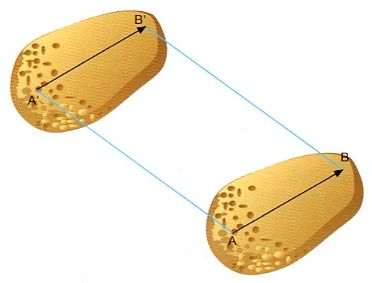
Moviment d’un sòlid en què tots els punts que el constitueixen experimenten el mateix desplaçament.
Si A i B representen les posicions inicials de dos punts qualssevol del sòlid, i A’ i B’ les corresponents als mateixos punts després d’efectuada una translació, s’acompleix B-A = B'-A’, B-A i B'-A’ essent els vectors Això vol dir que un desplaçament per translació és un desplaçament rígid Hom pot descompondre sempre el moviment genèric d’un cos, en un instant donat, en una translació i una rotació
reticle
Matemàtiques
Conjunt ordenat en el qual dos elements qualssevol tenen un suprem (la més petita de les fites superiors o elements majorants) i un ínfim (la més gran de les fites inferiors o elements minorants).
És anomenat també conjunt reticular Si C, ≤ és un “ordenat” que és reticle, donats a i b de C, existeix un element, anomenat suprem c = a ∪ b tal, que a ≤ c , b ≤ c , i si a < d i b < d és c < d i un element, dit ínfim , c = a ∩ b tal, que c < a, c < b i si d ≤a, d ≤ b , és d ≤ c El conjunt de parts d’un conjunt respecte a l’ordre definit per la inclusió és un reticle Exemple si A i B són dos conjunts qualssevol, el conjunt més petit que els conté és la seva reunió o…
regla dels signes
Matemàtiques
Regla que dona el signe del producte de dos nombres reals qualssevol.
És - a b = - ab = a -b - a - b = a b on a ∈ℝi b ∈ℝ, i pot ésser generalitzada a qualsevol anell commutatiu Hom pot enunciar-la dient que si els signes són iguals el producte és +, i si són diferents és -
proporcional
Matemàtiques
Dit de dues quantitats variables de raó constant fixa.
Així, hom diu, per exemple, que l’àrea del cercle és proporcional al quadrat del seu radi La quarta proporcional de tres nombres a, b i c és un nombre x tal que a/b = c/x la tercera proporcional de dos nombres a i b és el nombre x tal que a/b = b/x la mitjana proporcional entre dos nombres a i b és el nombre x tal que a/x = x/b Per exemple, 10 és la quarta proporcional de 1, 2, 5 1/2 = 5/10 4 és la tercera proporcional de 1, 2 1/2 = 2/4 i 2 és la mitjana proporcional de 1, 4 1/2 = 2/4 Dues quantitats…
borrèlia
Biologia
Gènere de bacteris mòbils, de l’ordre de les espiroquetals, que s’enrotllen en espiral, de 10 a 20 μm de llargada.
Contràriament a les altres espiroquetes es tenyeixen bé amb els colorants d’anilina Creixen malament en els medis de cultiu artificials, però bé en els embrions de poll B recurrentis, B duttonii, B turicatae, B parkeri, B hermisii són els agents causants de les diverses febres recurrents febre
funció d’acidesa
Química
Funció de l’acidesa a H S +
de les solucions d’un àcid en el solvent S, que dóna, per a cada composició de la solució, la tendència a cedir protons a una base.
Aquesta funció, introduïda per Hammett, és definida, per a una base de Brønsted elèctricament neutra B, per l’expressió on a i és l’activitat i f i el coeficient d’activitat de i f i = a i /C i , essent C i la concentració de i i pot ésser calculada per la fórmula on tant K A , que és la constant d’acidesa en el solvent S de l’àcid HB + , conjugat de B, com C B , i C H B + , que són concentracions, són experimentalment accessibles Si hom pot admetre tal com féu Hammett, basant-se en fets experimentals, que f B / f H B…
tríedre de Frenet
Matemàtiques
Tríedre trirectangle constituït pels vectors tangent, normal i binormal a una corba en un punt.
Donada una corba C , parametritzada per l’abscissa curvilínia s s dona la longitud de l’arc des d’un punt de referència de la corba, C s = x s , y s , z s , tríede ortonormal directe definit en cada punt P de C pels vectors tangent t , normal n i binormal b , l’expressió dels quals és t = d C s / ds P , ∥ t ∥=1 n = d t / ds /∥ d t / ds ∥ P , ∥ n ∥=1 b = t ∧ n , ∥ b ∥=1 El pla P , t , n és el pla osculador de la corba C en el punt P , el pla P , n , b és el pla normal de C en P , i el pla P , b , t és el pla…
equació de Beattie-Bridgman
Física
Equació que relaciona la pressió, el volum i la temperatura d’un gas real, vàlida dins un ampli interval de valors d’aquestes variables.
En la seva deducció, hom té en compte la interacció entre les molècules del gas S'escriu , essent A = A 0 1— a/v , B = B 0 1— b/v , ε = c/vT 3 , on p és la pressió, T la temperatura, v el volum, R la constant dels gasos, i A 0 , a , B 0 , b i c , constants típiques de cada gas
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- …
- Pàgina següent
- Última pàgina