Resultats de la cerca
Es mostren 5909 resultats
impuls
Tecnologia
Donada una força F(t) que actua sobre una partícula de massa m durant un interval T, magnitud definida per la fórmula I = ∫ T 0 F(t)dt
.
A partir de la segona llei de Newton hom obté que l’impuls és igual a l’increment del moment lineal o sia T = m v T - m v 0, on v és la velocitat de la partícula, resultat anomenat teorema de l’impuls En la dinàmica de les rotacions hom anomena impuls angular la magnitud I = ∫ T 0 M t dt , on M t és el moment resultant de les forces
convergència
Matemàtiques
Qualitat de convergent.
En el cas d’una successió de funcions hom pot parlar de convergència en diferents sentits, segons la topologia donada en el conjunt de funcions a considerar així, hi ha la convergència puntual una successió f n tendeix a f si, per a tot x on les f n estan definides, f n x té límit f x la convergència uniforme f n convergeix uniformement a f si, per a tot ε> 0, es dona un N tal, que n> N implica | f n x - f x |
polígon de forces
Física
Construcció gràfica que serveix per a trobar la resultant d’un sistema de forces qualsevol.
Si F 1 , F 2 , F 3 són les forces, la resultant R és obtinguda dibuixant vectors fixos representants de F 1 , F 2 , F 3 , de manera que l’extrem de cadascun sigui l’origen del següent R és el vector lliure representat pel vector fix que comença a l’origen de F 1 i acaba a l’extrem de F 3
llei de Bosanquet
Física
Llei que resulta d’observar l’analogia entre la definició de reluctància i la llei d'Ohm: la força magnetomotriu Fmd’un circuit magnètic és Fm = RmΦ, essent Rmla reluctància i Φ el flux magnètic de Fm.
discontinuïtat
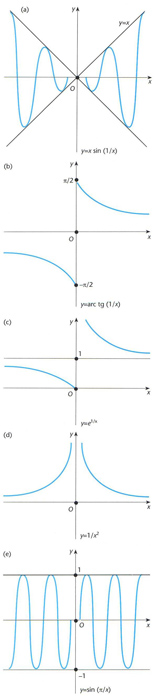
Discontinuïtat d’una funció: (a) discontinuitat evitable en x = 0, amb valor veritable y(0) = 0; (b) discontinuïtat de primera espècie infinita en x = 0, amb salt -2; (c) discontinuïtat de primera espècie infinita amb un punt d’infinit en x = 0; i (e) discontinuïtat de segona espècie finita en x = 0, per inexistència d’ambdós límits laterals quan x 0
© Fototeca.cat
Matemàtiques
Manca de continuïtat d’una funció en un punt o en un conjunt de punts, els quals són anomenats, per extensió, les discontinuïtats de la funció.
Atès que una funció f x és contínua en un punt a si i només si existeix i és igual a f a , la funció f x és discontínua en a si i només si no se satisfà alguna d’aquestes dues condicions, la qual cosa s’esdevé en els següents casos En primer lloc, pot passar que existeixi però que f a no existeixi f no sigui definida a a , o bé que aleshores, a és una discontinuïtat evitable , i la discontinuïtat és evitada redefinint el valor de f x al punt a tot assignant-li el valor el qual és anomenat valor veritable…
integració
Matemàtiques
Càlcul d’una integral.
Per a calcular integrals indefinides són útils, sovint, el mètode d’integració per substitució i el mètode d’integració per parts Segons el primer, hom fa x = φ t , i substitueix aquest valor a la integral ∫ f x dx = ∫fϕ t ϕ´ t dt , a fi de resoldre aquesta darrera més fàcilment El mètode d’integració per parts es basa en la relació → u dv = uv - que sigui de fàcil resolució Trobada la funció primitiva F x , la solució és ∫ f x dx = F x + C , on C és una constant La regla de Barrow proporciona un mètode general per a calcular…
espai vectorial
Matemàtiques
Grup abelià E
en el qual hi ha definida una llei de composició externa amb elements d’un cos K
, K
× E
→ E tal, que al parell (λ, e
) correspon l’element λ e
.
I acomplint-se les propietats λ + μ e = λ e + μ e , λ e + f = λ e + λ f , λμ e = λμ e i 1 e = e Els elements de E són anomenats vectors , i els elements de K , escalars Una part de E que sigui subgrup respecte a la suma i que sigui estable respecte al producte per qualsevol escalar, és anomenada subespai de E , i amb les mateixes operacions de E és un altre espai vectorial Si F és un subespai de E , hom pot definir congruències a E mitjançant la relació d’equivalència x ≡ y mòd F , si i només si la diferència x — y pertany a F…
integral de línia
Matemàtiques
Integral definida sobre al llarg d’una corba C a l’espai.
Donada una corba C a l’espai, parametritzada per l’assignació t ∈ a,b → r t = x t , y t , z t , i una funció vectorial f definida i fitada sobre la corba C , f C ⊂ℝ 2 →ℝ 3 , definida per l’assignació r → f r = f 1 r , f 2 r , f 3 r , la integral de línia és valor donat per la integral quan aquesta existeix Hom l’anomena integral de f al llarg de C
funció contínuament derivable a trossos
Matemàtiques
Funció f:[a,b]⊂ℝ→ℝtal que l’interval de definició [a,b] és la unió d’un nombre finit d’intervals tancats en què f és contínuament derivable.
escala de Fujita
Meteorologia
Escala per a la classificació de la intensitat dels tornados.
Els valors de la intensitat del vent en aquesta escala són F0 60-117 km/h F1 118-181 km/h F2 182-250 km/h F3 251-320 km/h F4 321-420 km/h F5 421-520 km/h En l’escala de Fujita també es fa referència als efectes i els danys que cal esperar per a cada grau d’intensitat del tornado
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- …
- Pàgina següent
- Última pàgina