Resultats de la cerca
Es mostren 2685 resultats
tangent d’un angle
Matemàtiques
Donats dos eixos perpendiculars x i y, i una circumferència de radi unitat centrada en el punt d’intersecció dels eixos (cercle goniomètric), i un segment que forma un angle α amb l’eix d’abcisses x, longitud del segment, perpendicular a l’eix d’abcisses, deteminat entre el punt de la circumferència de coordenades (1,0) i el punt en què aquest segment s’interseca amb el segment inclinat l’angle α en qüestió.
Aquesta longitud és la tangent de l’angle α, i és denotada per tgα És vàlida la següent igualtat tgα=sin α/cos α, on sin és el sinus d’un angle i cos és el cosinus d’un angle La tangent de l’angle α determinat entre dos segments qualssevol és la tangent de l’angle que, dibuixat sobre el cercle goniomètric, té la mateixa obertura que α Algunes fòrmules trigonomètriques relatives a la tangent d’un angle són tgα+β=tgα+tgβ/1-tgα- tgβ tg-α=-tgα tgα+tgβ- =sinα+β/cosα cosβ
teorema de Pitàgores
Matemàtiques
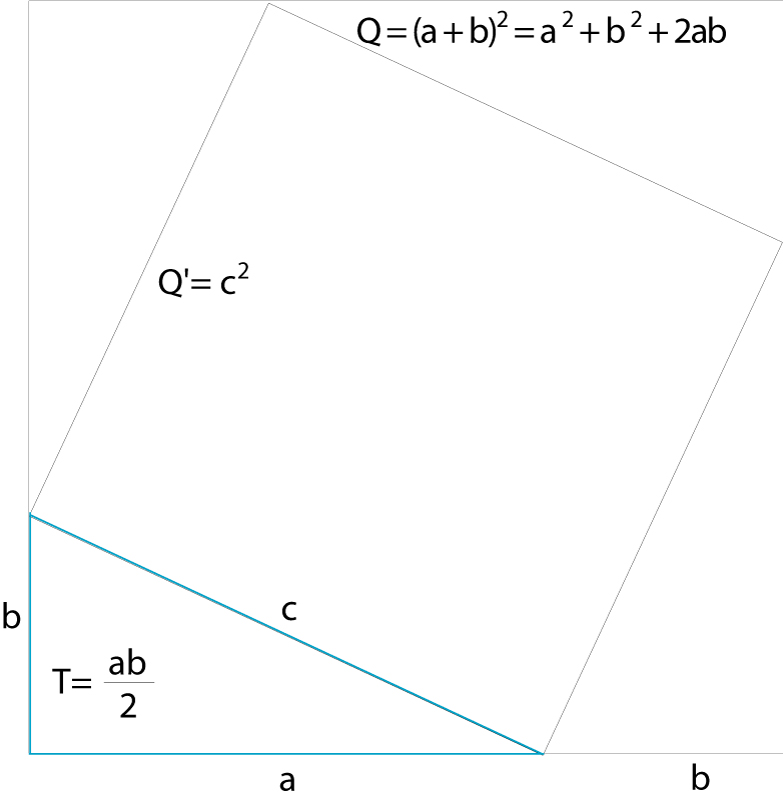
Teorema fonamental de la geometria segons el qual en un triangle rectangle l’àrea del quadrat que té per costat la hipotenusa és igual a la suma de les àrees dels quadrats que tenen per costat els catets.
Si a i b representen les longituds dels catets i c la longitud de la hipotenusa, el teorema Pitàgores és expressat per la igualtat c 2 = a 2 + b 2 Bé que la primera demostració del teorema sembla que fou feta pels membres de l’ escola pitagòrica Pitàgores vers l’any 550 aC, el teorema de Pitàgores, almenys en alguns casos particulars, ja era conegut pel poble egipci vers l’any 2000 aC, pels xinesos vers l’any 1100 aC i pels vedes vers l’any 800 aC D’altra banda, fou a partir del teorema que els pitagòrics descobriren que no n'hi ha prou amb els nombres enters i fraccionaris…
piragüisme
Esport
Esport consistent a navegar amb piragua, canoa o caiac.
Modalitat olímpica des del 1936, és practicada en piragües d’una, dues o quatre places dites K-1 5,20 m de longitud per 51 cm d’amplada i 12 kg de pes per a un sol tripulant, K-2 6,50 m de longitud, 55 cm d’amplada i 18 kg de pes per a dos tripulants i K-4 11 m de longitud, 60 cm d’amplada i 30 kg de pes per a quatre tripulants o en canoes d’una o dues places C-1 5,20 m de longitud, 75 cm d’amplada i 16 kg de pes per a un sol tripulant i C-2 6,50 m de longitud, 75 cm d’amplada i 20 kg de pes per a dos tripulants que remen…
peu
Física
Antiga mesura catalana de longitud.
Al Principat i a les Illes val 1/6 de la cana, o sia 0,259 m Al País Valencià val 1/3 de la vara, o sia 0,302 m El peu és relacionat amb el pam, de manera que 3 peus = 4 pams A les antigues constitucions de Catalunya el valor del peu fou adoptat en 0,2994 m
sector circular
Sector circular
Matemàtiques
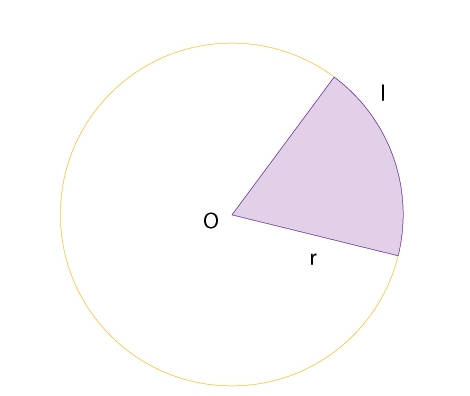
Part de cercle limitada per dos radis i l’arc comprès entre els seus extrems.
La seva superfície S pot ésser calculada a partir de la longitud l de l’arc i de la longitud r dels radis, mitjançant la fórmula S= 1/2 lr
tub acústic
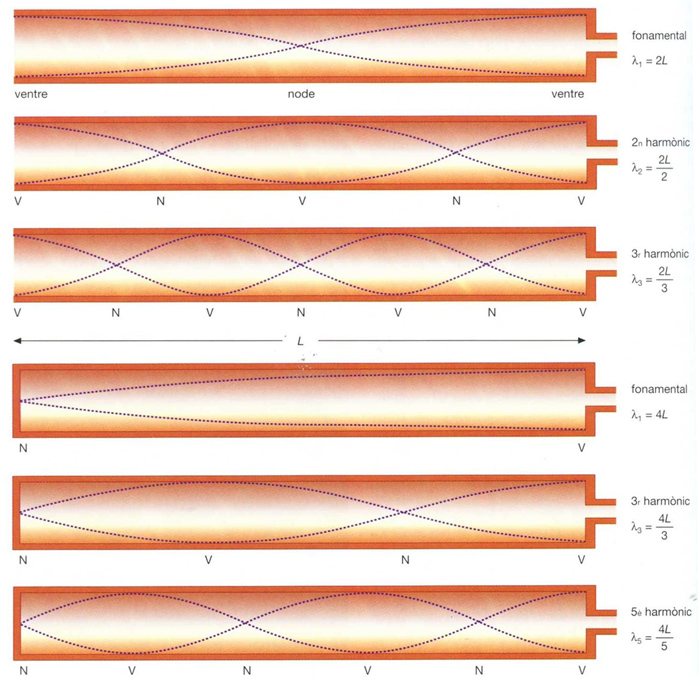
Vibracions en un tub: 1, obert (a, fonamental; b i c, harmònics); 2, tancat (a, fonamental; b i c, harmònics senars)
© Fototeca.cat
Física
Qualsevol tub de metall o de fusta, de secció quadrada, cònic o bé cilíndric, disposat de manera que l’aire de l’interior pugui vibrar i, així, pugui produir sons.
Les parets del tub són rígides, i a la base hi ha una embocadura per on és insuflat l’aire Això produeix la vibració d’aquest aire, les característiques de la qual depenen fonamentalment de les dimensions i de la forma del tub també varien segons que l’extrem superior sigui obert o tancat Quan l’aire del tub vibra, es produeixen —com en el cas de les cordes— ones estacionàries Si el tub és tancat per un extrem, les ones presenten en aquest punt un node, mentre que a l’extrem oposat apareix un ventre en aquest cas la longitud d’ona λ de la vibració val λ = 4 L, L essent la …
raig
Física
Direcció en què avança l’energia que es propaga en una ona lluminosa i, per extensió, en qualsevol ona electromagnètica.
En cada punt, aquesta direcció és normal al front de l’ona en el dit punt En el cas de la llum hom pot visualitzar-lo considerant un feix de llum prou estret a fi que les seves dimensions transversals siguin molt petites al costat de la seva longitud, però prou ample comparat amb la longitud d’ona de la llum a fi que no es produeixin fenòmens de difracció Segons la longitud d’ona, els raigs reben diferents noms espectre Els raigs lluminosos , corresponents a la llum visible, són els més coneguts en un extrem hi ha els raigs infraroigs infraroig i a l’altre els raigs ultraviolats…
Forth
Riu
Riu d’Escòcia.
Neix a les muntanyes Grampianes, passa per Stirling i desemboca a la mar del Nord, on forma un estuari de 83 km de longitud Fins a Alloa, a l’entrada de l’estuari, el riu té una longitud de 105 km
astròcit
Biologia
Cèl·lula de la neuròglia que es caracteritza per la possessió d’un gran nombre de prolongacions ramificades.
Hi ha dos tipus d’astròcits els astròcits de radiacions curtes , especialment abundants a la substància grisa, amb prolongacions de longitud aproximadament igual, i els astròcits de radiacions llargues , abundants a la substància blanca dels òrgans nerviosos, amb prolongacions de longitud variable
allargament
Tecnologia
Propietat que tenen determinats materials d’allargar-se en ésser sotmesos a càrregues o esforços de tracció.
En assaigs de materials, l’allargament és definit com l’augment de longitud respecte a la inicial que es produeix en la proveta, sotmesa a la tracció En fer l’assaig, la proveta, sota esforços creixents, experimenta un augment de la seva longitud fins que es produeix la ruptura
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- …
- Pàgina següent
- Última pàgina