Resultats de la cerca
Es mostren 5 resultats
intersecció
Matemàtiques
Conjunt format per elements que pertanyen alhora a dos conjunts o més.
La intersecció de dos conjunts, A i B , és denotada per A ∩ B , i es llegeix A intersecció B En geometria, hom parla d’interseccions entre corbes i superfícies
tangent d’un angle
Matemàtiques
Donats dos eixos perpendiculars x i y, i una circumferència de radi unitat centrada en el punt d’intersecció dels eixos (cercle goniomètric), i un segment que forma un angle α amb l’eix d’abcisses x, longitud del segment, perpendicular a l’eix d’abcisses, deteminat entre el punt de la circumferència de coordenades (1,0) i el punt en què aquest segment s’interseca amb el segment inclinat l’angle α en qüestió.
Aquesta longitud és la tangent de l’angle α, i és denotada per tgα És vàlida la següent igualtat tgα=sin α/cos α, on sin és el sinus d’un angle i cos és el cosinus d’un angle La tangent de l’angle α determinat entre dos segments qualssevol és la tangent de l’angle que, dibuixat sobre el cercle goniomètric, té la mateixa obertura que α Algunes fòrmules trigonomètriques relatives a la tangent d’un angle són tgα+β=tgα+tgβ/1-tgα- tgβ tg-α=-tgα tgα+tgβ- =sinα+β/cosα cosβ
sinus d’un angle
Matemàtiques
Donats dos eixos perpendiculars x i y, i un segment de longitud unitat OP que forma un angle α amb l’eix d’abscisses x, valor de la projecció de OP sobre l’eix y
.
Aquesta projecció és el sinus de l’angle α i és denotada per sinα El sinus de l’angle α determinat entre dos segments qualssevol és el sinus de l’angle que, dibuixat sobre aquest cercle goniomètric, té la mateixa obertura que α Algunes fórmules trigonomètriques relatives al sinus d’un angle són sinα+β = sinα cosβ - cosα sinβ sin-α = -sinα sinα sinβ = cosα-β - cosα+β/2 sinα + sinβ = 2 sinα+β/2 cosα-β/2 Entre el cosinus i el sinus d’un angle hi ha la relació fonamental cos 2 α+sin 2 α=1
cosinus d’un angle
Matemàtiques
Donats dos eixos perpendiculars x
i y
, i un segment de longitud unitat OP
que forma un angle α amb l’eix d’abscisses x
, valor de la projecció de OP
sobre l’eix x
.
Aquesta projecció és el cosinus de l’angle α i és denotada per cos α El cosinus de l’angle α determinat entre dos segments qualsevol és el cosinus de l’angle que, dibuixat sobre aquest cercle goniomètric, té la mateixa obertura que α Algunes fórmules trigonomètriques relatives al cosinus d’un angle són cosα+β=cosα cosβ-sinα sinβ cos-α= cosα cosαcosβ = cosα+β+cosα-β/2 cosα + cosβ = 2 cosα + β/2cosα - β/2 Entre el cosinus i el sinus d’un angle hi ha la relació fonamental cos 2 α + sin 2 α = 1
funció exponencial
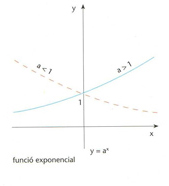
Funció exponencial
© Fototeca.cat
Matemàtiques
Funció contínua f
:ℝ→ℝ +
-{0} que satisfà f
( x
+ x
’) = f
( x
) f
( x
’), per a tot parell x,x
’∈ℝ, i f
(1)= a
, essent a
un nombre real concret que la caracteritza, anomenat base
.
És denotada per l’assignació x → a x És la funció inversa de la funció logarítmica de base Hom empra, especialment, la funció exponencial que té per base el nombre e aquesta és la inversa de la funció logarítmica neperiana ln e x = e l n x = x Quan hom no especifica la base, hom parla de funció exponencial o simplement d’exponencial, tot sobreentenent que es tracta de la funció exponencial de base e , i la nota e x o exp x Té la propietat d e x / dx = e x , i admet el desenvolupament en sèrie Aquesta sèrie convergeix també en el cos ℂ, la qual cosa permet de definir-hi la…