Resultats de la cerca
Es mostren 13 resultats
expansió
Física
Augment de volum que experimenta un fluid en disminuir la pressió que suporta.
L’expansió és reversible si es produeix mitjançant variacions infinitesimals de pressió aleshores el sistema passa per tots els estats d’equilibri successius En cas contrari l’expansió és irreversible Segons les condicions en què es produeix, hi ha variacions de treball extern, de calor o d’entropia
productivitat marginal
Economia
Variació de la quantitat produïda deguda a la modificació d’una petita quantitat de l’input variable.
En termes infinitesimals i considerant que la funció és contínua i derivable, la productivitat marginal coincidirà amb la derivada parcial de primer ordre PMg = ∂z/∂X v Ensems i amb una tecnologia determinada es pot afirmar d’acord amb el postulat de la llei de rendiment decreixent que ∂ 2 Z/∂X 2 v < O , és a dir, que per increments d' input els increments de l' output seran menors que proporcionals
Pierre Simon de Fermat

Retrat de Pierre Simon de Fermat
© Fototeca.cat
Matemàtiques
Història del dret
Advocat occità, sobresortí pels seus treballs matemàtics.
Estudià a Tolosa Introduí per primera vegada l’infinit en el càlcul, descobrí les propietats de diversos nombres i és considerat el creador de la moderna teoria dels nombres Amb Descartes, aplicà l’àlgebra a la geometria, i, amb Pascal, fundà la teoria de les probabilitats Aplicà el concepte de les variables infinitesimals als problemes de quadratura, de càlcul de màxims i mínims i a la construcció de tangents El 1679 el seu fill Samuel escriví Varia opera mathematica , on es recull l’obra de Fermat
coeficients calorimètrics
Física
Coeficients que expressen la quantitat de calor rebuda per la unitat de massa d’un cos en funció de les variacions de pressió P, volum V i temperatura T, quan una d’elles roman constant.
Són la calor específica a pressió constant C p , la calor específica a volum constant C v , la calor d’augment de pressió isoterma h , la calor de dilatació isoterma l i els coeficients, sense nom propi, λ i μ La calor rebuda per un sistema que experimenta unes variacions infinitesimals δ P , δ V i δ T és δ Q = C v δ T + l δ V , δ Q = C v δ T + h δ P i δ Q = λδ P +μδ V L’equació d’estat, fP,V,T=0, permet d’expressar tots els coeficients calorimètrics en termes de només C v i C p
elasticitat
Economia
Mesura de la sensibilitat d’una magnitud econòmica en modificar-se’n una altra de què depèn.
Matemàticament s’expressa com a quocient entre la variació relativa de la variable dependent x i la variació relativa de la independent y ε = Δ x/x /Δ y/y , formulació que, quan es refereix a variacions infinitesimals, és equivalent a la de la tangent de la corba en un punt L’anàlisi econòmica la utilitza per a estudiar el grau d’influència d’una variable respecte a una altra, fent abstracció d’altres condicionants, però condicionada per l’existència de béns substitutius Les més emprades són la de l’elasticitat de la demanda i l’oferta respecte al preu, la de la demanda i l’…
volum
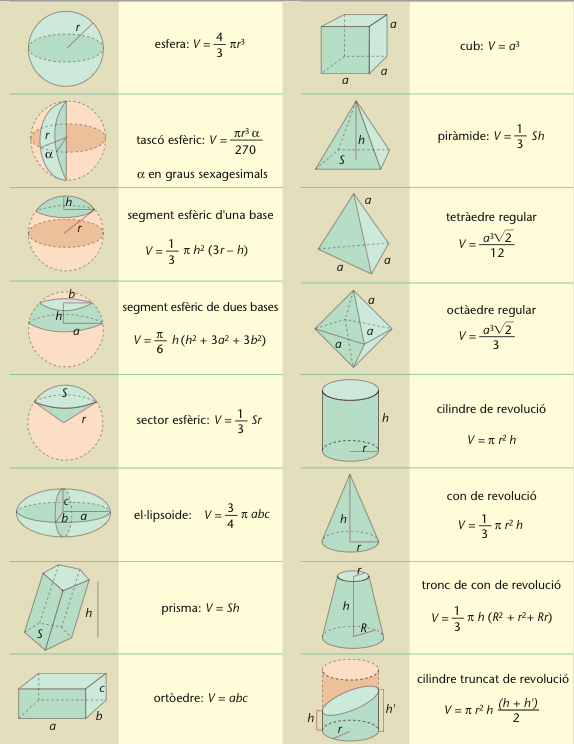
Fórmules per al càlcul de volums
© Fototeca.cat
Matemàtiques
Grandor o mesura de la porció de l’espai ocupada per un cos.
El volum és una mesura que a tota regió de l’espai de tres dimensions assigna un nombre real positiu, de manera que es compleix la propietat additiva, és a dir, que el volum d’un cos és igual a la suma dels volums de qualsevol partició que hom hagi fet en el cos divisió del cos en parts disjuntes Prenent com a base que el volum assignat a un cub de costat a és a 3 , el volum de qualsevol altre cos pot ésser calculat com l’ínfim de la suma dels volums dels cubs disjunts que plegats cobreixen el cos Així, el volum d’una figura plana és zero El volum dels cossos geomètrics simples pot ésser…
ortomòrfic | ortomòrfica
Matemàtiques
Dit de la transformació, representació, etc, d’una figura sobre una superfície conservant la forma dels seus elements infinitesimals.
És anomenada també conforme
element de superfície
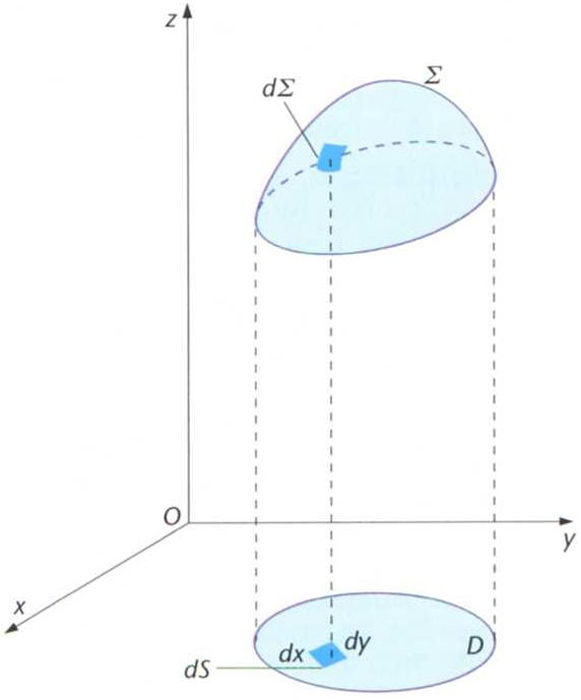
Element de superfície
© fototeca.cat
Matemàtiques
Cadascuna de les parts infinitesimals en què hom divideix una superfície a l’hora de calcular-ne l’àrea.
En coordenades cartesianes l’element de superfície dS val dS = dx dy , i en coordenades polars dS = ρ d ρ d θ L’àrea A d’una superfície regular z = f x,y que tingui com a projecció en el pla XOY un recinte S , és igual a la integral doble expressada per
mecànica de fluids
Física
Ciència que estudia l’equilibri i el moviment dels fluids i llur relació amb les forces que els produeixen o que s’hi oposen.
Aquesta denominació fou introduïda per Prandtl, el 1905, en sintetitzar i aprofundir els estudis que hom feia, separadament, en el camp de la hidrodinàmica i de l’aerodinàmica teòriques i en relacionar-los íntimament amb fets experimentals Després, fou aplicada també a l’estudi de fluids més complexos que els usuals, la qual cosa conduí a l’aplicació de diferents models matemàtics i a una anàlisi acurada de diversos fenòmens Els primers estudis teòrics eren fets sobre fluids perfectes , on no hi hagués resistència al lliscament relatiu de les capes fluides adjacents…
trencament de simetria
Física
Fenomen pel qual fluctuacions infinitesimals d’un sistema proper a un punt crític en determinen l’evolució en travessar una transició de fase; típicament, la transició ocorre entre un estat desordenat, o amb certa simetria (per exemple, rotacional), a un sistema més ordenat o amb menys simetria.
Un exemple en matèria condensada és el trencament de simetria que es dóna quan un material ferromagnètic és refredat per sota de la temperatura de Curie, moment en què el material adquireix una magnetització en una direcció espacial particular Arguments similars s’apliquen en altres casos, com ara en cosmologia, per a explicar l’abundància actual de matèria respecte de l’antimatèria Pels treballs en aquest darrer camp, YNambu rebé el premi Nobel de física 2008