Resultats de la cerca
Es mostren 163 resultats
axioma de Borel-Lebesgue
Matemàtiques
Propietat d’un espai topològic E que se satisfà quan de tot recobriment obert de E hom pot extreure un subrecobriment finit.
Un espai topològic que satisfà l’axioma de Borel-Lebesgue és anomenat espai compacte
categoria
Matemàtiques
Estructura algèbrica composta per una família d’objectes matemàtics i per una família de morfismes entre aquests objectes, tal que satisfà les següents propietats.
per a tot parell X,Y d’objectes de la categoria existeix un conjunt Hom X,Y, anomenat conjunt de morfismes de X en Y, tal que HomX,Y = HomX’,Y’ si i només X=X’ i Y=Y’ i, per a tot triplet X,Y,Z d’objectes de la categoria, existeix una aplicació Hom Y,Z x HomX,Z→HomX,Z, anomenada composició de morfismes, que satisfà l’associativitat i l’existència d’una identitat a cada HomX,X és a dir, existeix un morfisme 1 x tal que per a tot f de HomX,X se satisfà Els objectes d’una categoria no han de formar necessàriament un conjunt, sino una classe així, per exemple, la…
funció homogènia
Matemàtiques
Funció f:E→ℝ, on E és un espai vectorial, que satisfà f(λx) per a tot x∈E i λ∈ℝ.
Hom diu, concretament, que f és una funció homogènia de grau α, i α∈ℝés el grau d’homogeneïtat de f En el cas que E =ℝ n una funció homogènia de grau α satisfà f λ x 1 ,, x n =λ α -
funció periòdica
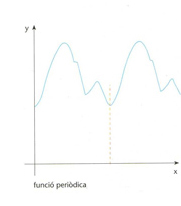
Funció periòdica
© Fototeca.cat
Matemàtiques
Funció f
: D
⊂ℝ→ℝtal que existeix un nombre T
∈ℝ-{0} que satisfà que, per a tot x
∈ D, x
+ T∈ D
i f
( x
+ T
)= f
( x
).
Hom diu aleshores que T és un període de la funció f bé que hom anomena, pròpiament, període al més petit nombre T que satisfà les condicions esmentades En són exemples les funcions trigonomètriques sinus i cosinus que tenen un període 2π
element crisipià
Lògica
Matemàtiques
En una lògica de proposicions, tota proposició P que satisfà simultàniament el principi del tercer exclòs (P ⌉ P≡1) i el principi de (no)-contradicció (P ⌉ P≡0).
Quan tots els elements d’una lògica de proposicions són crisipians, hom diu que la lògica és crisipiana Tota lògica bivalent principi de bivalència és necessàriament crisipiana, però no a l’inrevés La qualitat d’ésser crisipiana una lògica és de caire sintàctic Des d’un punt de vista semàntic hom pot dir que una lògica és crisipiana quan satisfà el principi de bivalència
relació
Matemàtiques
Lligam entre diversos elements d’un conjunt.
Per tal de precisar aquesta idea intuïtiva, hom defineix la relació com a qualsevol subconjunt d’un producte cartesià del conjunt amb ell mateix és a dir, que els elements són relacionats si formen un element del subconjunt En general, en una relació intervé un nombre determinat d’elements n així, una relació d’ordre entre els elements és un subconjunt del producte de n conjunts A El tipus de relació més freqüent és aquella en què n = 2, anomenada relació binària , que és un subconjunt de A × A Si els dos elements són a i b , hom diu que a R b , o que a és relacionat amb b —o sia, que a,b…
desigualtat de Clausius
Física
Relació que expressa que en un procés cíclic, al llarg del qual un sistema termodinàmic rep les quantitats de calor dQ1..., dQn, de fonts tèrmiques mantigudes a les temperatures respectives T1... Tn, la suma de les quantitats dQi/Ti estesa a un cicle és negativa o nul·la: ∫dQ/T ≤0.
La igualtat se satisfà quan el cicle és reversible
funció normada
Matemàtiques
Funció de norma unitat.
Per a la norma més corrent, satisfà ∫ b a | f x | 2 dx =1