Resultats de la cerca
Es mostren 83 resultats
corba bipolar
Matemàtiques
Corba plana que pot ésser definida com el conjunt de punts les coordenades bipolars dels quals, respecte a dos focus F i F´, satisfan una determinada relació, anomenada equació bipolar de la corba.
P ex, l’ellipse és determinada pel fet que els seus punts satisfan r + r' = 2 a , essent a el semieix major i r i r' les distàncies dels punts als focus F i F'
quàdrica

Matemàtiques
Dit de la superfície algèbrica de segon grau les coordenades (x, y, z) dels punts de la qual satisfan una equació del tipus la qual hom acostuma a escriure, fent servir notació matricial, .
Si notem la primera matriu associada a les coordenades d’un punt per α, i la segona formada pels coeficients de la quàdrica per β, aleshores l’anterior expressió pot escriure's com α t βα ═ 0, on α t és la matriu transposada de α Dos punts M 0 i M 1 són dits conjugats respecte a una quàdrica quan llurs matrius satisfan α t 0 βα 1 = 0 Un pla és anomenat pla polar d’un punt respecte a una quàdrica quan és format pels punts conjugats del punt considerat Hom anomena centre de la quàdrica qualsevol punt conjugat de tots els punts de l’infinit, i plans diametrals , els plans polars…
polinomis de Legendre
Matemàtiques
Polinomis en ℝ donats per l’expressió genèrica
.
Satisfan la fórmula de recurrència n +1 P n + 1 x - 2n+1 P n x + nP n - 1 x =0, i són solucions de l' equació diferencial de Legendre , 1- x 2 y´´ - 2 xy ´ + n n +1 y = 0 Els primers polinomis són P 0 x = 1, P 1 x = x , P 2 x = 3 x 2 -1 /2 Satisfan la següent ortogonalitat on és el símbol de Kronecker
polinomis de Laguerre
Matemàtiques
Polinomis en ℝ donats per l’expressió genèrica
Satisfan la fórmula de recurrència n +1 L n ₊₁ x + x-2n-1 L n x + n L n ₋₁ x = 0, i són solucions de l' equació diferencial de Laguerre, xy n + 1- x y’ + ny = 0 Els primers polinomis són L₀ x = 1, L₁ x = 1- x, L₂ x = 1-2 x + x 2 /2 Satisfan la següent ortogonalitat on és el símbol de Kronecker
polinomis d’Hermite
Matemàtiques
Polinomis en ℝ donats per l’expressió genèrica
Satisfan la fórmula de recurrència H n + 1 x - 2 xH n x + 2 nH n - 1 x = 0, i són solucions de l' equació diferencial d’Hermite, y n - 2 xy + 2 ny = 0 Els primers polinomis són H 0 x = 1, H 1 x = 2 x , H 2 x = 4 x 2 -2, etc Satisfan la següent ortogonalitat on δ p q és el símbol de Kronecker
distributiu | distributiva
Matemàtiques
Dit d’una llei de composició interna quan satisfà determinades propietats.
En un conjunt E dotat de dues lleis de composició internes o operacions, una d’elles és distributiva respecte a l’altra quan se satisfan les següents propietats si a * b° c = a * b ° a * c hom diu que * és distributiva per l’esquerra respecte a °, si b° c* a = b * a ° c * a llavors, * és distributiva per la dreta respecte a °, i si se satisfan ambdues condicions hom diu que * és distributiva respecte a ° A ℝ, la multiplicació és distributiva respecte a la suma, però no a l’inrevés
equació funcional
Matemàtiques
Relació imposada a una funció.
Una tal relació defineix una funció o família de funcions que satisfan aquella relació
axiomes independents
Matemàtiques
Conjunt d’axiomes tals que cap d’ells no es pot deduir dels altres.
Per a demostrar aquesta independència es donen models que satisfan certs axiomes, però no els altres
con de llum
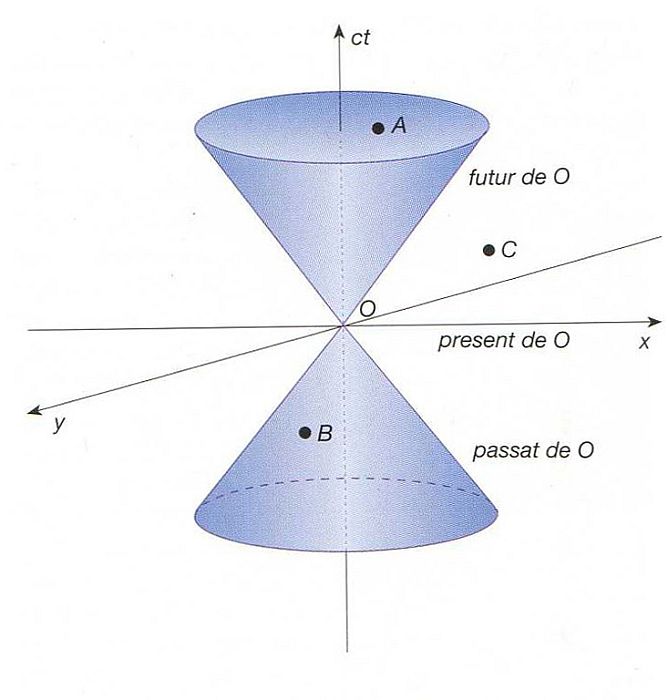
Representació en dues dimensions espacials del con de llum tetradimensional de l’esdevenimentO
©
Física
A l’espaitemps tetradimensional de la relativitat especial, figura que palesa gràficament el significat dels conceptes passat, present i futur d’un esdeveniment qualsevol O.
És una superfície hipercònica de dos fulls formada pels esdeveniments separats de l’esdeveniment O origen de coordenades per un 4-interval tipus-llum Δ s 2 = c 2 Δ t 2 - |Δ r | 2 = 0 Els punts A de l’interior del con de llum que satisfan Δ s 2 > 0 amb Δ t > 0, formen el con del futur o simplement, el futur de l’esdeveniment 0 els punts B de l’interior del con de llum que satisfan Δ s 2 > 0 amb Δ t < 0, formen el con del passat O , simplement, el passat de O els punts C de l’exterior del con de llum, que satisfan Δ s 2 < 0, formen el…
lleis de De Morgan
Lògica
Matemàtiques
En lògica d’enunciats, lleis donades per les equivalències següents: no(P i Q) = (no P) o (no Q), i no(P o Q) = (no P) i (no Q).
En teoria de conjunts, lleis donades per les igualtats i on les barreres indiquen els conjunts complementaris Les lleis de De Morgan se satisfan en tota Boole, àlgebra de
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- Pàgina següent
- Última pàgina