Resultats de la cerca
Es mostren 46 resultats
teoremes de Guldin
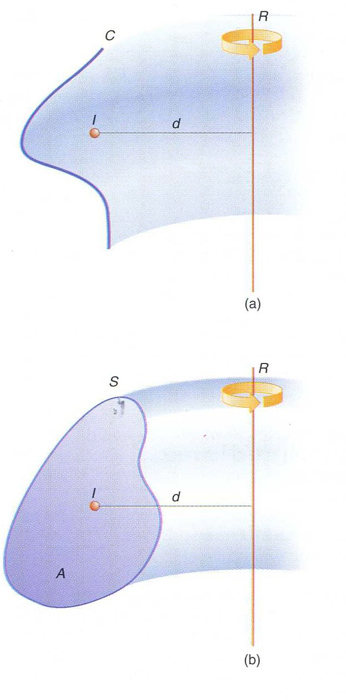
teoremes de Guldin: (a) primer teorema; (b) segon teorema
© fototeca.cat
Matemàtiques
Teoremes que relacionen el centre de massa d’una corba o d’una superfície amb l’àrea o el volum, respectivament, que generen en girar al voltant d’un eix.
Segons el primer teorema de Guldin , donada una corba plana C , de longitud l , que gira al voltant d’una recta R del seu pla, la qual no talla, l’àrea A de la superfície de revolució que genera és A = 2π dl , on d és la distància des del centre de massa I de la corba a la recta R en el cas purament geomètric, el centre de massa és calculat assignant la mateixa “massa” a tots els punts de la corba matemàtica en el cas físic, el centre de massa és el del sistema de masses puntuals de la corba material El segon teorema de Guldin afirma que, donada una superfície plana S , d’àrea A , que gira al…
Escala logarítmica, nomografia (Gunter); teoremes de centroides (Paul Guldin); geometria, trigonometria, π, loxodròmies (Snell).
Escala logarítmica, nomografia Gunter teoremes de centroides Paul Guldin geometria, trigonometria, π, loxodròmies Snell
Pappus d’Alexandria
Matemàtiques
Matemàtic grec.
És autor d’una Collecció matemàtica en vuit volums, d’un gran valor, tant per la immensa documentació aportada com per l’extensa recopilació que suposa dels treballs anteriors d’altres matemàtics Enuncià, a més, alguns teoremes geomètrics propis, com el teorema del centroide teoremes de Guldin i el teorema de l’hexàgon
teorema
Matemàtiques
Qualsevol proposició matemàtica que pot ésser demostrada a partir d’unes hipòtesis, uns axiomes o altres proposicions demostrades anteriorment.
Les proposicions prèvies de demostració breu que precedeixen un teorema de demostració més complicada són dites lemes , mentre que les conseqüències que es deriven del teorema són anomenades corollaris Hom anomena també teorema qualsevol conclusió general que ja ha estat demostrada Una conjectura , en canvi, és una proposició que hom creu certa però en desconeix la demostració Hi ha nombrosos teoremes coneguts, com ara el de Pitàgores, el de Tales, el del valor mitjà, etc Dos teoremes són anomenats recíprocs quan cadascun té per hipòtesi la conclusió de l’altre
postulat
Lògica
Proposició fonamental d’un sistema deductiu que ni és evident ni pot ésser demostrada.
Tradicionalment el postulat era contraposat a l'axioma, pel fet de no ésser evident ni universalment acceptat, i al teorema, pel fet de no ésser demostrable Actualment, tanmateix, hom assimila el postulat a l’axioma, per tal com pot ésser posada en qüestió la idea d’evidència Més que no el seu caràcter apriorístic, el que hom entén avui com a propi del postulat és la posició primària que aquest ocupa en un sistema formal El sistema de postulats d’una teoria ha d’ésser elegit de tal manera que totes les proposicions de la teoria puguin ésser deduïdes per una cadena de raonaments d’aquells…
Ludwig Sylow
Matemàtiques
Matemàtic noruec.
Fou professor a Oslo Estudià els grups i subgrups, dels quals establí teoremes fonamentals El 1881 publicà els treballs d’Abel
Karl Wilhelm Feuerbach
Matemàtiques
Matemàtic alemany.
Fou professor de matemàtiques a Erlangen Demostrà diferents teoremes que reben el seu nom, i estudià la geometria del cercle, del triangle i de la piràmide triangular
lema de Zorn
Matemàtiques
Lema establert pel matemàtic nord-americà d’origen alemany Max Zorn, segons el qual en tot conjunt ordenat inductiu (és a dir, on tot subconjunt totalment ordenat té una fita superior) existeix un element maximal.
Aquest lema o axioma és “equivalent lògicament” a l' axioma de Zermelo i al teorema de Zermelo i d’altres d’enunciats L’ús del lema de Zorn és molt freqüent, en especial per a demostrar teoremes d’existència com ara el referent a la base d’un espai vectorial
Georg Ferdinand Frobenius
Matemàtiques
Matemàtic alemany.
Fou professor a la Universitat de Berlín Investigà en les branques més elevades de l’àlgebra, en connexió amb la teoria de les funcions i dels grups Els nombrosos teoremes que duen el seu nom representen un enriquiment de l’àlgebra clàssica i constitueixen un dels punts de partida de l’àlgebra moderna