Resultats de la cerca
Es mostren 97 resultats
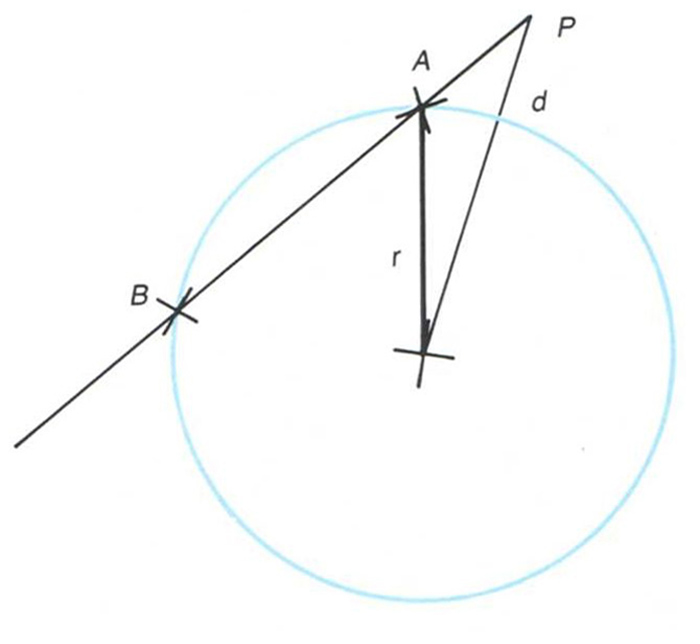
potència d’un punt respecte a una circumferència
fototeca.cat
©
Matemàtiques
Donats un punt P
i una circumferència, producte de les distàncies del punt P
als dos punts A
i B
que una recta que passa per P
determina sobre la circumferència.
Es verifica que el dit producte, és independent de la recta traçada fototecacat ©
Friedrich Paschen
Física
Físic alemany.
Fou professor a Tübingen, Bonn i Berlín Estudià les ratlles espectrals, els raigs X i les descàrregues elèctriques en els gasos, i verificà experimentalment la teoria atòmica relativista de Sommerfeld
espai afí
Matemàtiques
Caràcter d’un conjunt A
respecte a un espai vectorial E
, amb el qual hom pot definir una aplicació E
× A → A.
Es compleix que per a tot parell v , a , on v pertany a E i a pertany a A , li correspon l’element v + a de A , i que verifica les propietats L’espai afí s’estudia dins el context de la geometria analítica
postulat d’Arquimedes
Matemàtiques
Proposició segons la qual si hom pren dos elements qualssevol, α i β, d’un conjunt que tingui estructura de semigrup ordenat, existeix un nombre enter n tal que na ⩾ β, és a dir, hi ha múltiples del petit majors que el gran.
L’estructura de semigrup és la que té condicions mínimes per a poder enunciar el postulat d’Arquimedes Generalment, però, hom parla de cossos arquimedians Els conjunts en els quals es verifica aquesta proposició són anomenats conjunts arquimedians per exemple, els nombres reals i els altres conjunts no arquimedians per exemple, els nombres transfinits
absorbància
Física
Magnitud que caracteritza una substància pel que fa a l’absorció d’energia radiant.
Ve donada per A = log I 0 / I , essent I 0 i I les intensitats radiants incident i transmesa, respectivament Si la llum és monocromàtica es verifica, generalment, que A d , essent d el gruix travessat llei de Lambert i, en el cas de solucions, A cd , on c és llur concentració llei de Beer
pantalla
Construcció i obres públiques
Element bidimensional de formigó, massís o poc perforat, disposat en vertical com a part de l’estructura d’un edifici, per tal de millorar-ne la resistència i la rigidesa davant de les accions horitzontals de sisme i vent.
La contribució resistent d’una pantalla es verifica fonamentalment en la direcció de la seva dimensió principal en planta, essent negligible la contribució en la direcció perpendicular al seu plànol És habitual coŀlocar conjunts de pantalles i combinar-ne l’orientació, de manera que resultin eficients davant de forces horitzontals que actuïn segons totes les direccions possibles
pesador | pesadora
Funcionari o, en general, persona que verifica el pes.
espai projectiu
Matemàtiques
Conjunt de classes d’equivalència, P, de punts de Rn + 1 — {Ō}.
On R n + 1 és un espai vectorial de dimensió n + 1, obtingudes per la relació ''dos punts x i x' estan relacionats si i només si estan alineats amb l’origen’, és a dir, si es verifica x ' 1 ,, x' n + 1 = r x 1 ,, x n 1 per a tot nombre real r ≠ 0 El seu estudi pertany a la geometria projectiva
azeotròpic | azeotròpica
Química
Dit de la mescla de dos o més líquids volàtils que a una pressió determinada té un punt d’ebullició constant i es destil·la sense canvi de composició destil·lació), és a dir, que el vapor té la mateixa composició que el líquid.
En un principi hom cregué que aquesta mescla constituïa un compost definit pels components de la mescla, però no és així, puix que si l’ebullició es verifica a una pressió diferent no solament canvia el punt d’ebullició sinó també la composició Una mescla azeotròpica és anomenada de punt d’ebullició màxim quan aquest és més alt que el dels seus components azeotropia positiva i de punt d’ebullició mínim quan és més baix azeotropia negativa
condició d’aplanetisme d’Abbe
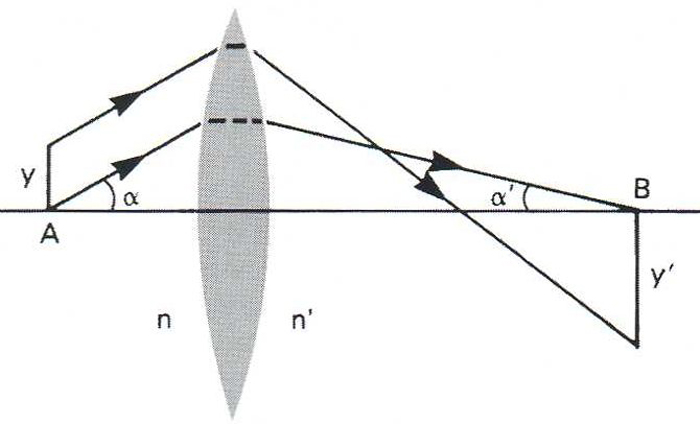
Condició d’aplanetisme d’Abbe. A punt objecte; B punt imatge; y objecte; y' imatge; α angle objecte; α' angle imatge
© fototeca.cat
Física
Relació que ha de complir un sistema òptic perquè sigui aplanètic.
L’expressió que la dóna és n y sinα = n'y' sinα’, essent n i n' els índexs de refracció del medi objecte i imatge, i y i y' les dimensions transversals d’objecte i imatge, i α i α’ els angles que forma una mateix raig que havent sortit del punt objecte A arribi al punt imatge B Un sistema és aplanètic si verifica aquesta condició per a qualsevol punt de l’eix i unes certes dimensions transversals És anomenada també condició del sinus
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina